Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

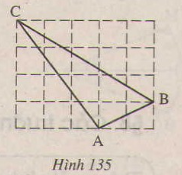
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34
Giải:
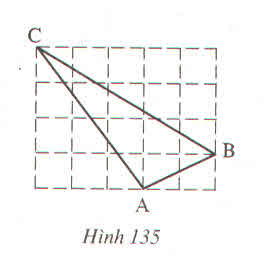
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34

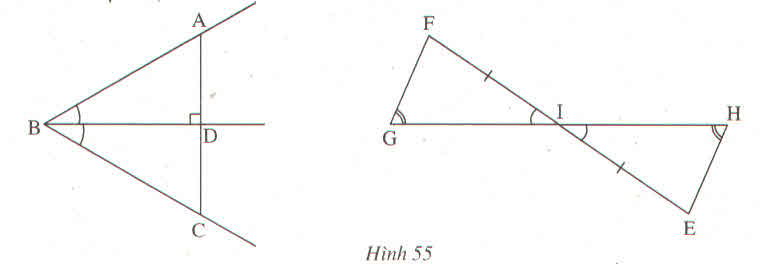
-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH


Ta có : AB=AC
=> \(\Delta ABC\) là tam giác vuông cân tại A ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{ABC}=A\widehat{CB}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{ABC}=A\widehat{CB}=45^0\)
=> \(\widehat{CBD}=\widehat{A}+\widehat{BCA}=135^0\) ( góc ngoài của tam giác )
Ta lại có:
BD=BC
=> \(\Delta BCD\) cân tại B ( vì tam giác có 2 cạnh bằng nhau )
=> \(\widehat{BDC}=\widehat{BCD}\) ( hai cạnh đáy của tam giác cân )
=> \(\widehat{BDC}=\widehat{BCD}=\dfrac{\left(180^0-135^0\right)}{2}=\dfrac{45^0}{2}=22,5^0\)
Mà \(\widehat{ACD}=\widehat{BCA}+\widehat{BCD}\)
=> \(\widehat{ACD}=45^0+22,5^0=67,5^0\)
Vậy trong \(\Delta ACD\) có :
\(\left\{{}\begin{matrix}\widehat{A}=90^0\\\widehat{ADC}=22,5^0\\\widehat{ACD}=67,5^0\end{matrix}\right.\)


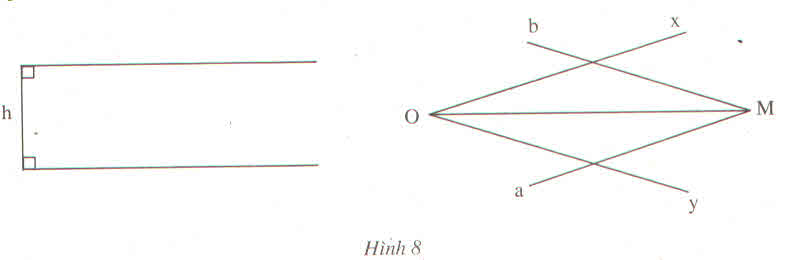
Kẻ MH vuông góc với Ox, MK vuông góc với Oy
=>MH và MK là chiều rộng của thước hai lề
=>MH=MK
=>M thuộc tia phân giác của góc xOy


Hướng dẫn:
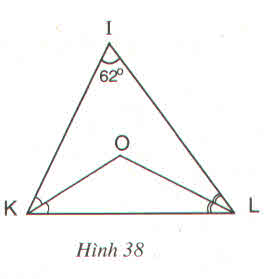
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210
c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL
a, Áp dụng định lí tổng 3 góc trong ΔIKL, ta có:
∠I + ∠IKL + ∠ILK= 180 độ
⇒ ∠IKL + ∠ILK= 180 độ - ∠I
OK, OL là phân giác của các góc K, L nên:
∠OKL= 1/2∠IKL, ∠OLK= 1/2∠ILK
⇒ ∠OKL + ∠OLK= 1/2 (∠IKL + ∠ILK)
= 1/2 . (180 độ - ∠I)
Áp dụng định lí tổng 3 góc trong ΔOKL có:
∠ KOL + ∠OKL + ∠OLK = 180 độ
⇒ ∠KOL= 180 độ - (∠OKL + ∠OLK)
= 180 độ - 180- ∠I / 2= 180 + ∠I/2
Mà ∠I= 62 độ nên:
∠KOL= 180 +62/2= 121 độ
b, Ta có: 3 đường phân giác trong tam giác đồng quy.
Mà 2 đường phân giác KO, LO cắt nhau tại O
⇒ OI là tia phân giác của ∠KIL
⇒ ∠KIO= 1/2 ∠KIL= 1/2. 62 độ= 31 độ
c, O là giao điểm 3 đường phân giác của ΔIKL. Áp dụng định lí 3 đường phân giác
Vậy O cách đều 3 cạnh của ΔIKL