Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

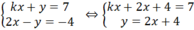
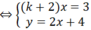
Với k + 2 ≠ 0 ⇔ k ≠ -2 thì hệ phương trình có nghiệm :
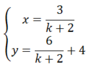
Ta có:
P = x 2 + y 2 = x 2 + 2 x + 4 2
= 5 x 2 + 16 x + 16
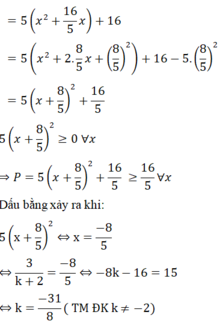
Vậy với k = (-31)/8 thì biểu thức P = x 2 + y 2 đạt giá trị nhỏ nhất

hệ pt <=> 2x-4y = 6m+2
2x+y = m+2
<=> 2x-4y-2x-y = 6m+2-m-2
2x+y = m+2
<=> -5y=5m
2x+y = m+2
<=> x=m+1 và y=-m
Khi đó : x^2-y^2 = (m+1)^2-(-m)^2 = m^2+2m+1-m^2 = 2m+1
Hình như đề sai hoặc thiếu rùi bạn ơi !
Tk mk nha

\(\left\{{}\begin{matrix}mx+y=7\\2x-y=-4\end{matrix}\right.\left(1\right)\)
Ta có: \(2x-y=-4\)
\(\Rightarrow y=2x+4\)
\(P=x^2+y^2=x^2+\left(2x+4\right)^2=x^2+4x^2+16x+16\)
\(P=5x^2+16x+16=5\left(x^2+2.\frac{8}{5}x+\frac{64}{25}\right)+\frac{16}{5}\)
\(P=5\left(x+\frac{8}{5}\right)^2+\frac{16}{5}\)
Do: \(\left(x+\frac{8}{5}\right)^2\ge0\Rightarrow5\left(x+\frac{8}{5}\right)^2+\frac{16}{5}\ge\frac{16}{5}\)
\(P_{Min}=\frac{16}{5}\Leftrightarrow x=-\frac{8}{5}\) Mà: \(y=2x+4\Rightarrow y=\frac{4}{5}\)
Thay \(x,y\) vào phương trình đề cho ta được:
\(m\left(-\frac{8}{5}\right)+\frac{4}{5}=7\)
\(\Leftrightarrow m=-\frac{31}{8}\)
Vậy nếu \(m=-\frac{31}{8}\) thì \(P\) đạt \(Min=\frac{16}{5}\)

ta có : \(\left\{{}\begin{matrix}mx+y=7\\2x-y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=7-mx\\2x-7+mx=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=7-mx\\x=\dfrac{11-mx}{2}\end{matrix}\right.\)
\(\Rightarrow P=x^2+y^2=\dfrac{\left(11-mx\right)^2}{4}+\left(7-mx\right)^2\)
\(=\dfrac{121-22mx+m^2x^2}{4}+49-14mx+m^2x^2\)
\(=\dfrac{5m^2x^2-78mx+317}{4}\)
\(=\dfrac{5m^2x^2-2.\sqrt{5}mx+\dfrac{78}{2\sqrt{5}}+\dfrac{1521}{5}+\dfrac{64}{5}}{4}\)
\(=\dfrac{\left(\sqrt{5}mx-\dfrac{78}{2\sqrt{5}}\right)^2+\dfrac{64}{5}}{4}\)
ta có : \(P\) nhỏ nhất khi \(\dfrac{\left(\sqrt{5}mx-\dfrac{78}{2\sqrt{5}}\right)^2+\dfrac{64}{5}}{4}\) nhỏ nhất
\(\Leftrightarrow\left(\sqrt{5}mx-\dfrac{78}{2\sqrt{5}}\right)^2+\dfrac{64}{5}\) nhỏ nhấtta có : \(\left(\sqrt{5}mx-\dfrac{78}{2\sqrt{5}}\right)^2+\dfrac{64}{5}\ge\dfrac{64}{5}\forall mx\)
khi \(\sqrt{5}mx-\dfrac{78}{2\sqrt{5}}=0\Leftrightarrow m=\dfrac{39}{5x}\)
khi đó ta có : \(P=\dfrac{\dfrac{64}{5}}{4}=\dfrac{16}{5}\)
vậy .............................................................................................
