Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do đó \(\Delta BOF=\Delta DOH\left(g.c.g\right)\) suy ra \(OH=OF\)
Chứng minh tương tự, \(OE=OG\). Do đó EFGH là hình bình hành.
Ta lại có \(OH\perp OE\) (tia phân giác của hai góc kề bù). Do đó hình bình hành EFGH là hình thoi.

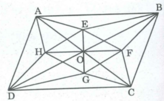
Ta có: ∠ (AOB) = ∠ (COD) (đối đỉnh)
∠ (EOB ) = 1/2 ∠ (AOB) (gt)
∠ (COG) = 1/2 ∠ (COD) (gt)
Suy ra: ∠ (EOB ) = ∠ (COG)
∠ (EOB) + ∠ (BOC) + ∠ (COG) = 2 ∠ (EOB) + ∠ (BOC)
Mà ∠ (AOB ) + ∠ (BOC) = 180 0 ( kề bù).Hay 2 ∠ (EOB) + ∠ (BOC ) = 180 0
Suy ra: E,O,G thẳng hàng
Ta lại có: ∠ (BOC) = ∠ (AOD ) ( đối đỉnh)
∠ (HOD) = 1/2 ∠ (AOD) (gt)
∠ (FOC) = 1/2 ∠ (BOC) (gt)
Suy ra: ∠ (HOD) = ∠ (FOC)
∠ (HOD) + ∠ (COD ) + ∠ (FOC) = 2 ∠ (HOD) + ∠ (COD)
Mà ∠ (AOD) + ∠ (COD) = 180 0 ( kề bù). Hay 2 ∠ (HOD) + ∠ (COD) = 180 0
Suy ra: H, O, F thẳng hàng
∠ (ADO) = ∠ (CBO) ( so le trong)
∠ (HDO) = ∠ (FBO) ( chứng minh trên)
OD = OB ( t/chất hình bình hành)
∠ (HOD) = ∠ (FOB ) ( đối đỉnh)
Do đó: ∆ BFO = ∆ DHO (g.c.g)
⇒ OF = OH
∠ (OAB) = ∠ (OCD) ( so le trong)
∠ (OAE) = 1/2 ∠ (OAB ) (gt)
∠ (OCG) = 1/2 ∠ (OCD) (gt)
Suy ra: ∠ (OAE) = ∠ (OCG)
Xét ∆ OAE và ∆ OCG,ta có :
∠ (OAE) = ∠ (OCG) ( chứng mình trên)
OA = OC ( t/chất hình bình hành)
∠ (EOA) = ∠ (GOC) ( đối đỉnh)
Do đó: ∆ OAE= ∆ OCG (g.c.g) ⇒ OE = OG
Suy ra tứ giác EFGH là hình bình hành ( vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù) hay EG ⊥ FH
Vậy tứ giác EFGH là hình thoi
Fan Twice ak?
Mk cx la once ne (bias Momo)