Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

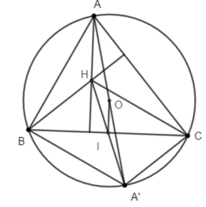
Gọi A’ là điểm đối xứng với A qua O. Ta có: BH // A’C suy ra BHCA’ là hình bình hành do đó HA’ cắt BC tại trung điểm I của BC. Mà O là trung điểm của AA’ suy ra OI là đường trung bình của tam giác AHA’ suy ra A H → = 2 O I →
Chọn đáp án C

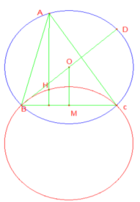
Theo t/c đường tròn, do M là trung điểm BC \(\Rightarrow OM\perp BC\)
Áp dụng định lý Pitago:
\(OM=\sqrt{OC^2-CM^2}=\sqrt{R^2-\left(\dfrac{BC}{2}\right)^2}=3\)
\(\Rightarrow\) Quỹ tích M là đường tròn tâm \(\left(O;3\right)\)
Mặt khác do G là trọng tâm tam giác ABC
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\) G là ảnh của M qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là ảnh của \(\left(O;3\right)\) qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là đường tròn bán kính \(\dfrac{2}{3}.3=2\)

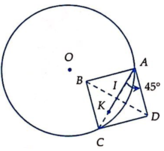
- Theo tính chất hình bình hành : BA=DC \(\Rightarrow\overrightarrow{AB}=\overrightarrow{CD}\). Nhưng theo giả thiết A,B cố định , cho nên \(\overrightarrow{AB}\) cố định . Ví C chạy trên (O;R) , D là ảnh của C qua phép tịnh tiến theo \(\overrightarrow{AB}\) , cho nên D chạy trên đường tròn O’ là ảnh của đường tròn O
- Cách xác định (O’) : Từ O kẻ đường thẳng // với AB , sau đó dựng véc tơ \(\overrightarrow{OO'}=\overrightarrow{AB}\). Từ O’ quay đường tròn bán kính R , đó chính là đường tròn quỹ tích của D.

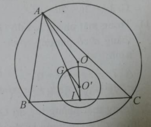
B, C cố định nên trung điểm I của BC cũng cố định. G là trọng tâm tam giác ABC nên ta có I G → = 1 / 3 I A → ⇒ có phép vị tự I tỉ số k = 1/3 biến A thành G. A chạy trên (O) nên G chạy trên (O’) ảnh của O qua phép vị tự trên.
Đáp án C