Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của đồ thị và đường thẳng là \(-x+m=\frac{x^2-1}{x}\)
\(\Leftrightarrow2x^2-mx-1=0\) (*) (vì x = 0 không là nghiệm của (*))
Vì ac < 0 nên phương trình (*) luôn có 2 nghiệm phân biệt khác không
Do đó đồ thị và đường thẳng luôn cắt nhau tại hai điểm phân biệt :
\(A\left(x_1;-x_1+m\right);B\left(x_2;-x_2+m\right)\)
\(AB=4\Leftrightarrow\sqrt{\left(x_2-x_1\right)^2+\left(-x_2+m+x_1+m\right)^2}=4\)
\(\Leftrightarrow2\left(x_2-x_1\right)^2=16\)
\(\Leftrightarrow\left(x_2+x_1\right)^2-4x_2x_1=8\)
Áp ụng định lý Viet ta có : \(\begin{cases}x_2+x_1=\frac{m}{2}\\x_2x_1=-\frac{1}{2}\end{cases}\)
\(AB=4\Leftrightarrow\frac{m^2}{4}+2=8\Leftrightarrow m=\pm2\sqrt{6}\)
Vậy \(m=\pm2\sqrt{6}\) là giá trị cần tìm

Phương trình hoành độ giao điểm của \(\left(C_m\right)\) và đường thẳng y = -1 là :
\(x^4-\left(3m+2\right)x^2+3m=-1\Leftrightarrow\left(x^2-1\right)\left(x^2-3m-1\right)=0\)
Đường thẳng y = -1 cắt \(\left(C_m\right)\) tại 4 điểm phân biệt có hoành độ nhỏ hơn 2 khi và chỉ khi :
\(0 < 3m+1 < 4\) và \(3m+1\ne1\)
\(\Leftrightarrow\)\(-\frac{1}{3}< m\)< 1 và \(m\ne0\)

a) y′=3x+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0y′=3x2+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0
hoặc x2=−2m+63x2=−2m+63
Xảy ra hai trường hợp đối với dấu của y':
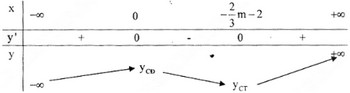
Rõ ràng, để hàm số có điểm cực đại tại x = -1 ta phải có
x2=−2m+63=−1⇔m=−32x2=−2m+63=−1⇔m=−32
(Chú ý : trường hợp x1 = x2 thì hàm số không có cực trị).
b) (Cm) cắt Ox tại x = -2 ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔ m=−53m=−53

Phương trình hoành độ giao điểm của đồ thị với trục hoành là :
\(x^3-2x^2+\left(1-m\right)x+m=0\left(1\right)\)
Biến đổi tương đương phương trình này :
\(\left(1\right)\Leftrightarrow x^3-2x^2+x-mx+m=0\)
\(\Leftrightarrow x\left(x^2-2x+1\right)-m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-x-m\right)=0\Leftrightarrow x=1\) hoặc \(x^2-x-m=0\left(2\right)\)
Gọi \(x_1,x_2\) là nghiệm của phương trình (2) thì :
\(t^2+x_1^2+x_2^2< 4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2< 3\Leftrightarrow m< 1\) (*)
Yêu cầu bài toán tương đương với (2) có hai nghiệm phân biệt \(x_1;x_2\ne1\) thỏa mãn điều kiện (*)
\(\Leftrightarrow\begin{cases}\Delta=1+4m>0\\1^2-1-m\ne0\\m< 1\end{cases}\)\(\Leftrightarrow\begin{cases}-\frac{1}{4}< m< 1\\m\ne0\end{cases}\)

Ta có \(d:y=mx-m-2\)
Hoành độ giao điểm là nghiệm của phương trình :
\(\frac{x-3}{1-x}=mx-m-2\Leftrightarrow\begin{cases}x\ne1\\mx^2-\left(2m+1\right)x+m-1=0\end{cases}\)
Điều kiện để cắt nhau tại hai điểm phân biệt là : \(\begin{cases}m\ne0\\m>-\frac{1}{8}\end{cases}\)
Gọi \(M\left(x_1;y_1\right);N\left(x_2;y_2\right)\) khi đó \(\begin{cases}x_1+x_2=\frac{2m+1}{m}\\x_1x_2=\frac{m-1}{2}\end{cases}\)
Ta có \(\overrightarrow{AM}=-2\overrightarrow{AN}\Rightarrow x_1=3-2x_2\)
Từ đó ta có m = 1
Hoành độ giao điểm của đường thẳng y = −3x + 9/2 với đồ thị của (1) thỏa mãn phương trình
Ta có (2) ⇔ x 3 /3 − (m − 1) x 2 + mx = 0 (2)
⇔ x[ x 2 − 3(m − 1)x + 3m] = 0
Để (2) có ba nghiệm phân biệt thì phương trình f(x) = x 2 – 3(m – 1)x + 3m = 0 phải có hai nghiệm phân biệt khác 0, tức là: