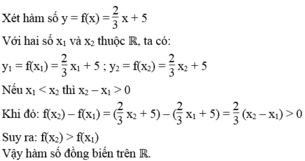Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có : x1<x2 suy ra 3x1<3x2 suy ra f(x1)<f(x2)
Suy ra y=f(x)=3x đồng biến trên R

\(\text{Ta có:}-m^2+m-4\\ =-\left(m^2-m+4\right)\\ =-\left[\left(m^2-m+\dfrac{1}{4}\right)+\dfrac{15}{4}\right]\\ =-\left(m-\dfrac{1}{2}\right)^2-\dfrac{15}{4}\le-\dfrac{15}{4}< 0\)
Vậy HSNB trên R
\(-m^2+m-4\)
\(=-\left(m^2-m+4\right)\)
\(=-\left(m^2-m+\dfrac{1}{4}+\dfrac{15}{4}\right)\)
\(=-\left(m-\dfrac{1}{2}\right)^2-\dfrac{15}{4}< 0\forall m\)
Vậy: Hàm số nghịch biến trên R

Gọi x1, x2 là hai giá trị của x (x1>x2)
Ta có: x1>x2\(\Leftrightarrow\)-2x1<-2x2 \(\Leftrightarrow\)f(x1) < f(x2)
Vì x1>x2 mà f(x1) < f(x2) suy ra hàm số nghịch biến trên tập hợp số thực R


f(x1)=3x1f(x1)=3x1
f(x2)=3x2f(x2)=3x2
Theo giả thiết, ta có:
x1<x2⇔3.x1<3.x2x1<x2⇔3.x1<3.x2 ( vì 3>03>0 nên chiều bất đẳng thức không đổi)
⇔f(x1)<f(x2)⇔f(x1)<f(x2) (vì f(x1)=3x1;f(x1)=3x1;f(x2)=3x2)f(x2)=3x2)
Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên RR.
Chú ý:
Ta cũng có thể làm như sau:
Vì x1<x2x1<x2 nên x1−x2<0x1−x2<0
Từ đó: f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0
Hay f(x1)<f(x2)f(x1)<f(x2)
Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên R
Do \(x_1< x_2\Rightarrow3x_1< 3x_2\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Hàm số \(f\)đồng biến trên \(ℝ\)khi :
\(\forall x_1,x_2\inℝ\): \(x_1< x_2\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
=> Hàm số đã cho đồng biến trên \(ℝ\)

Cho x các giá trị bất kì x 1 , x 2 sao cho x 1 < x 2
= > x 1 - x 2 < 0
Ta có:
f x 1 = 3 x 1 ; f x 2 = 3 x 2 ⇒ f x 1 − f x 2 = 3 x 1 − 3 x 2 = 3 x 1 − x 2 < 0 ⇒ f x 1 < f x 2
Vậy với x 1 < x 2 ta được f ( x 1 ) < f ( x 2 ) nên hàm số y = 3x đồng biến trên tập hợp số thực R.

Cho x các giá trị bất kì x1, x2 sao cho x1 < x2
=> x1 - x2 < 0
Ta có: f(x1) = 3x1 ; f( x2) = 3x2
=> f(x1) - f(x2) = 3x1 - 3x2 = 3(x1 - x2) < 0
=> f(x1) < f(x2)
Vậy với x1 < x2 ta được f(x1) < f(x2) nên hàm số y = 3x đồng biến trên tập hợp số thực R.

Với x 1 , x 2 là hai giá trị bất kì của x thuộc R, ta có:
y 1 = f( x 1 ) = 4 - 2/5 x 1 ; y 2 = f( x 2 ) = 4 - 2/5 x 2
Nếu x 1 < x 2 thì x 1 - x 2 < 0. Khi đó ta có:
y 1 - y 2 = (4 - 2/5 x 1 ) - (4 - 2/5 x 2 )
= (-2)/5( x 1 - x 2 ) > 0. Suy ra y 1 > y 2
Vậy hàm số đã cho là hàm nghịch biến trên R.