Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

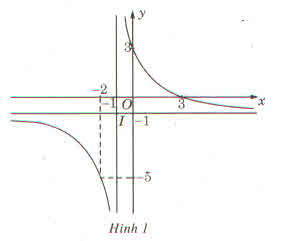
a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)

1, Đổi chỗ 3 viên ở 3 đỉnh tam giác: viên dưới cùng lên đỉnh trên cùng, 2 viên ngoài cùng ở 2 bên đảo xuốn đáy
2, 8-6+2=4; 12-5+8=15; 13-10+15=18. x=15
3,
*) \(5^3+5=130;3^3+3=30;2^3+2=10;1^3+1=2\)
*) 2+3=8 hay 2.(2+3)-2=8
4+5=32 hay 4.(4+5)-4=32
5+8=60 hay 5.(5+8)-5=60
6+7=72 hay 6.(6+7)-6=72
7+8= 7.(7+8)-7=98

a: Để A là số nguyên thì \(x-1\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{2;0;4;-2\right\}\)
b: Để B là số nguyên thì \(2x-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{1;0\right\}\)(do x là số nguyên)
c: Để C là số nguyên thì \(3x-3+10⋮x-1\)
\(\Leftrightarrow x-1\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
hay \(x\in\left\{2;0;3;-1;6;-4;11;-9\right\}\)
d: Để D là số nguyên thì \(4x-1⋮x-3\)
\(\Leftrightarrow x-3\in\left\{1;-1;11;-11\right\}\)
hay \(x\in\left\{4;2;14;-8\right\}\)

Lời giải:
PT hoành độ giao điểm:
\(mx+2m+1-\frac{2x+1}{x+1}=0\Leftrightarrow mx^2+x(3m-1)+2m=0\)
Để hai ĐTHS cắt nhau tại hai điểm $A,B$ thì \(m\neq 0\) và:
\(\Delta=(3m-1)^2-8m^2=m^2-6m+1>0\)
Khi đó áp dụng hệ thức Viete có \(\left\{\begin{matrix} x_1+x_2=\frac{1-3m}{m}\\ x_1x_2=2\end{matrix}\right.\)
Ta có:
\(d(A,Ox)=d(B,Ox)\Leftrightarrow |mx_1+2m+1|=|mx_2+2m+1|\)
TH1: \(mx_1+2m+1=mx_2+2m+1\Leftrightarrow x_1=x_2\)
\(\Rightarrow x_1=x_2=\sqrt{2}\Rightarrow \frac{1-3m}{m}=2\sqrt{2}\) kéo theo \(m=\frac{1}{2\sqrt{2}+3}\) (không thỏa mãn đk của \(\Delta)\)
TH2: \(mx_1+2m+1=-(mx_2+2m+1)\Leftrightarrow m(x_1+x_2)+4m+2=0\)
\(\Leftrightarrow 3+m=0\Rightarrow m=-3\) (t/m)
Vậy $m=-3$

\(y'=2x^2-6\left(m+1\right)x+9\)
Để hàm số có cực đại, cực tiểu
\(\Delta'=9\left(m+1\right)^2=3.9>0\)
\(=\left(m+1\right)^2-3>0\)
\(\Leftrightarrow m\in\left(-\infty;-1-\sqrt{3}\right)\cup\left(-1+\sqrt{3};+\infty\right)\)
Ta có : \(y=\left(\frac{1}{3}x-\frac{m+1}{3}\right)\left(3x^2-6\left(m+1\right)x+9\right)-2\left(m^2+2m-2\right)x+4m+1\)
Gọi tọa độ điểm cực đại và cực tiểu là \(\left(x_1;y_1\right)\) và \(\left(x_2;y_2\right)\)
=> \(y_1=-2\left(m^2+2m-2\right)x_1+4m+1\)
\(y_2=-2\left(m^2+2m-2\right)x_2+4m+1\)
Vậy đường thẳng đi qua 2 điểm cực đại và cực tiểu là
\(y=-2\left(m^2+2m-2\right)x+4m+1\)
Vì 2 điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng \(y=\frac{1}{2}x\) ta có điều kiện cần là :
\(\left[-2\left(m^2+2m-2\right)\right]\frac{1}{2}=-1\)
\(\Leftrightarrow m^2+2m-2=1\)
\(\Leftrightarrow m^2+2m-3=0\)
\(\Leftrightarrow\begin{cases}m=1\\m=-3\end{cases}\)
Theo định lí Viet ta có \(\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=3\end{cases}\)
Khi m =1 => phương trình đường thẳng đi qua 2 điểm cực đại và cực tiểu là
\(y=-2x+5\)
Tọa độ trung điểm cực đại và cực tiểu là :
\(\begin{cases}\frac{x_1+x_2}{2}=\frac{4}{2}=2\\\frac{y_1+y_2}{2}=\frac{-2\left(x_1+x_2\right)+10}{2}=1\end{cases}\)
Tọa độ trung điểm cực đại và cực tiểu là (2;1) thuộc đường thẳng \(y=\frac{1}{2}x\Rightarrow m=1\) thỏa mãn
Khi m=-3 phương trình đường thẳng đi qua 2 điểm cực đại và cực tiểu là y=-2x-11
(làm tương tự cách như trên)

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

a) y′=3x+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0y′=3x2+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0
hoặc x2=−2m+63x2=−2m+63
Xảy ra hai trường hợp đối với dấu của y':
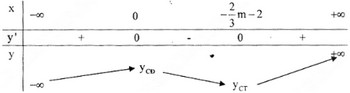
Rõ ràng, để hàm số có điểm cực đại tại x = -1 ta phải có
x2=−2m+63=−1⇔m=−32x2=−2m+63=−1⇔m=−32
(Chú ý : trường hợp x1 = x2 thì hàm số không có cực trị).
b) (Cm) cắt Ox tại x = -2 ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔ m=−53m=−53





Chọn D