Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng C. (-1,1)

y = 2x2 + 2mx + m -1 (Cm). Đây là hàm số bậc hai, đồ thị là parabol quay bề lõm lên phía trên.
a) m = 1 ⇒ y = 2x2 + 2x
Tập xác định D = R
\(\lim\limits_{x\rightarrow+\infty}y\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty\)
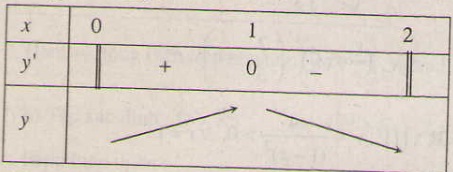
Bảng biến thiên:
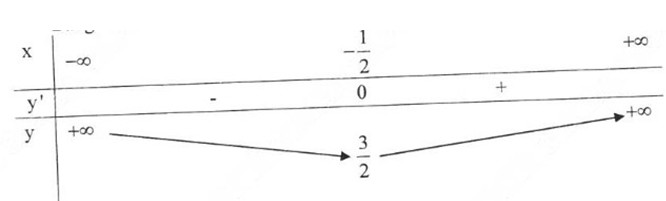
Đồ thị hàm số:
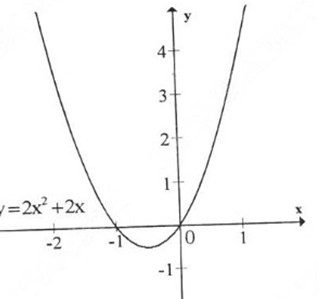
b) Tổng quát y = 2x2 + 2mx + m -1 có tập xác định D = R
y′=4x+2m=0⇔\(x=-\dfrac{m}{2}\).
Suy ra y’ > 0 với \(x>-\dfrac{m}{2}\) và \(y'< 0\) với \(x< -\dfrac{m}{2}\) tức là hàm số nghịch biến trên \(\left(-\infty;\dfrac{-m}{2}\right)\) và đồng biến trên \(\left(-\dfrac{m}{2};+\infty\right)\)
i) Để hàm số đồng biến trên khoảng (-1, +∞) thì phải có điều kiện (−1,+∞)∈(−\(\dfrac{m}{2}\),+∞)
Hay \(-\dfrac{m}{2}< -1\)\(\Leftrightarrow m>2\)
ii) Hàm số đạt cực trị tại \(x=\dfrac{m}{2}\)
Để hàm số đạt cực trị trong khoảng (-1, +∞), ta phải có:
\(-\dfrac{m}{2}\in\left(-1;+\infty\right)\) hay \(-\dfrac{m}{2}>-1\Leftrightarrow m< 2\).
c) (Cm) luôn cắt Ox tại hai điểm phân biệt
⇔ phương trình 2x2 + 2mx + m – 1 = 0 có hai nghiệm phân biệt.
Ta có:
Δ’ = m2 – 2m + 2 = (m-1)2 + 1 > 0 ∀m
Vậy (Cm) luôn cắt O x tại hai điểm phân biệt.

Đáp án C
Dựa vào bảng biến thiên, hàm số đã cho nghịch biến trên khoảng (-1;1)

*Xét hàm số: y= -x3 + 2x2 – x – 7
Tập xác định: D = R
\(y'\left(x\right)=-3x^2+4x-1\); \(y'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\end{matrix}\right.\)
y’ > 0 với và y’ < 0 với \(x \in ( - \infty ,{1 \over 3}) \cup (1, + \infty )
Vậy hàm số đồng biến trong (\(\dfrac{1}{3}\),1)(\(\dfrac{1}{3}\),1) và nghịch biến trong (−∞,13)∪(1,+∞)(−∞,13)b) Xét hàm số: \(y=\dfrac{x-5}{1-x}\).
Tập xác định: D = R{1}
\(y'=\dfrac{-4}{\left(1-x\right)^2}< 0,\forall x\in D\)
Vậy hàm số nghịch biến trong từng khoảng (-∞,1) và (1, +∞)

Câu 1: Điều kiện \(D=\left(-\infty;0\right)U\left(1;+\infty\right)\)
\(y'=\frac{\sqrt{x^2-x}-x.\frac{2x-1}{2\sqrt{x^2-x}}}{x^2-x}=\frac{-x}{2\left(x^2-x\right)\sqrt{x^2-x}}\)
Ta thấy \(y'< 0\) trên \(\left(1;+\infty\right)\), suy ra hàm số nghịch biến trên \(\left(1;+\infty\right)\).
Câu 2:
\(y'=1+\frac{2x}{\sqrt{2x^2+1}}=\frac{2x+\sqrt{2x^2+1}}{\sqrt{2x^2+1}}\)
Xét bất phương trình:
\(2x+\sqrt{2x^2+1}< 0\)
\(\Leftrightarrow\sqrt{2x^2+1}< -2x\)
\(\Leftrightarrow\hept{\begin{cases}x< 0\\2x^2+1< 4x^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 0\\x< \frac{-\sqrt{2}}{2}\left(h\right)x>\frac{\sqrt{2}}{2}\end{cases}}\Leftrightarrow x< \frac{-\sqrt{2}}{2}\)
Vậy hàm số nghịch biến trên \(\left(-\infty;\frac{-\sqrt{2}}{2}\right)\).
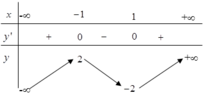
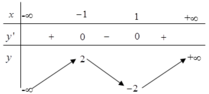
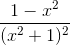 => y' = 0 ⇔ x=-1 hoặc x=1.
=> y' = 0 ⇔ x=-1 hoặc x=1.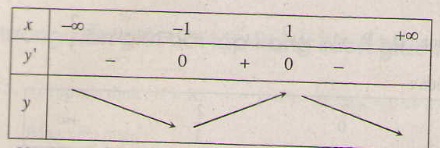


Chọn C
Từ bảng biến thiên ta thấy hàm số đã cho