DS
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 4 2017
a) Vẽ đồ thị hàm số y = x2.
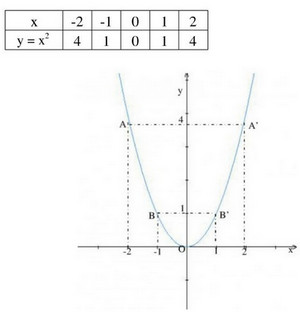
b) Ta có y = f(x) = x2 nên
f(-8) = (-8)2 = 64; f(-1,3) = (-1,3)2 = 1,69; f(-0,75) = (-0,75)2 = 0,5625; f(1,5) = 1,52 = 2,25.
c) Theo đồ thị ta có:
(0,5)2 ≈ 0,25
(-1,5)2 ≈ 2,25
(2,5)2 ≈ 6,25
d) Theo đồ thị ta có: Điểm trên trục hoành √3 thì có tung độ là y = (√3)2 = 3. Suy ra điểm biểu diễn √3 trên trục hoành bằng 1,7. Tương tự điểm biểu diễn √7 gồm bằng 2,7.
C
19 tháng 4 2017
a. Vẽ được rồi nên thôi
Hai điểm A(-2, 2) và B(1, 1/2)
b. Đường thẳng AB có PT: x + 2y - 2 = 0.
c. Diện tích tam giác ABC = \(\frac{1}{2}\)AB x d(C/AB)
AB cố định. => Diện tích tam giác ABC lớn nhất khi d(C/AB) lớn nhất
Điểm C có tọa độ (x; \(\frac{x^2}{2}\))
d(C/AB) = \(\frac{\left|x+2\frac{x^2}{2}-2\right|}{\sqrt{1^2+2^2}}\)
d(C/AB) đạt max khi \(\left|x+x^2-2\right|\) đạt max (vì C thuộc cung AB nên -2 < x < 1)
Ta có x2 + x - 2 = (x + 2)(x - 1)
với -2 < x < 1 => x2 + x - 2 < 0
=> \(\left|x^2+x-2\right|\)= -x2 - x + 2 (khi 2- < x < 1)
Vậy, d(C/AB) đạt max khi -x2 - x + 2 đạt max (khi 2- < x < 1)
-x2 -x + 2 = -(x + \(\frac{1}{2}\))2 + \(\frac{1}{4}\) + 2
= -(x +\(\frac{1}{2}\))2 + 9/4 >= 9/4
Vậy, d(C/AB) đạt max khi x = -\(\frac{1}{2}\)
Thay x = \(-\frac{1}{2}\)vào (P): y = \(\frac{x^2}{2}\)
Vậy, Điểm C: (\(-\frac{1}{2}\); \(\frac{1}{8}\))
TA
10 tháng 5 2018
Bạn ơi, câu a có hàm số đâu ?
b)
1/ PT hoành độ giao điểm của \(y=2x^2\) và \(y=3x+2\) là nghiệm của PT: (Câu này mình sẽ không ghi nữa vì đều phải ghi NTN nên mình chỉ ghi PT luôn, không ghi câu này nữa)
\(2x^2=3x+2\)
\(\Leftrightarrow\) \(2x^2-3x-2=0\)
(\(a=2\) ; \(b=-3\) ; \(c=-2\) )
Ta có: \(\Delta=b^2-4ac=\left(-3\right)^2-4.2.\left(-2\right)=25>0\)
\(\Rightarrow\) \(\sqrt{\Delta}=\sqrt{25}=5\)
\(\Rightarrow\) PT đã cho có 2 nghiệm phân biệt (2 giao điểm)
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3+5}{2}=2\) ; \(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3-5}{2.2}=-\dfrac{1}{2}\)
Với \(x_1=2\) thì \(y=2.2^2=8\)
Tương tự \(x_2\) . Ta được 2 giao điểm là (tự đặt tên)
2/ \(x^2=x-2\) (Bạn coi lại chỗ này nhé!)
\(\Leftrightarrow\) \(x^2-x+2=0\)
(\(a=1\) ; \(b=-1\) ; \(c=2\))
Ta có: \(\Delta=b^2-4ac=\left(-1\right)^2-4.1.2=-7< 0\)
\(\Rightarrow\) Không có giao điểm giữa 2 đường thẳng này
3/ \(\dfrac{1}{2}x^2=2x-2\)
\(\Leftrightarrow\) \(\dfrac{1}{2}x^2-2x+2=0\)
(\(a=\dfrac{1}{2}\) ; \(b'=-1\) ; \(c=2\) )
Ta có: \(\Delta'=b'^2-ac=\left(-1\right)^2-\dfrac{1}{2}.2=0\)
\(\Rightarrow\) PT đã cho có nghiệm kép (1 giao điểm)
\(x=\dfrac{c}{a}=2\)
Với \(x=2\) thì \(y=\dfrac{1}{2}.2^2=2\)
4/ \(-2x^2=3x+1\)
\(\Leftrightarrow\) \(2x^2+3x+1=0\) (Nhát ghi hệ số a b c quá !!)
Ta có: \(\Delta=b^2-4ac=3^2-4.2.1=1>0\)
\(\Rightarrow\) \(\sqrt{\Delta}=\sqrt{1}=1\)
\(\Rightarrow\) \(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-3+1}{2.2}=-\dfrac{1}{2}\) ; \(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-3-1}{2.2}=-1\)
Với \(x_1=-\dfrac{1}{2}\) thì \(y=-2.\left(-\dfrac{1}{2}\right)^2=-\dfrac{1}{2}\)
Tương tự \(x_2\)
5/ \(-x^2=x-2\)
\(\Leftrightarrow\) \(x^2+x-2=0\)
Ta có: \(a+b+c=1+1-2=0\)
\(\Rightarrow\) \(x_1=1\) ; \(x_2=\dfrac{c}{a}=2\)
Với \(x_1=1\) thì \(y=-1^2=-1\)
Tương tự \(x_2\)
6/ Như 3/
17 tháng 4 2018
b, Xác định tọa độ giao điểm
1. Tọa độ giao điểm giữa (P) y=2x2 và (d) y=3x+2 là nghiệm phương trình y = y <=> 2x2- 3x -2=0 giải phương trình trên với biệt thức là ra thôi
Những câu khác làm tương tự thôi, dạng này đơn giản thôi, do mình không biết denta nên không giải tiếp được. có gì thì cứ hỏi nhé
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 4 2020
Bài 1:
a/ Bạn tự giải
b/ \(\Delta'=\left(m+1\right)^2-m^2-2=2m-1>0\Rightarrow m>\frac{1}{2}\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+2\end{matrix}\right.\)
\(x_1^2+x_2^2=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4\left(m+1\right)^2-2\left(m^2+2\right)-10=0\)
\(\Leftrightarrow2m^2+8m-10=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-5\left(l\right)\end{matrix}\right.\)
Bài 2:
a/ Bạn tự giải
b/ Phương trình hoành độ giao điểm:
\(-x^2=2x-3\Leftrightarrow x^2+2x-3=0\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=-1\\x=-3\Rightarrow y=-9\end{matrix}\right.\)
Vậy hai giao điểm là \(\left(1;-1\right)\) và \(\left(-3;-9\right)\)