Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

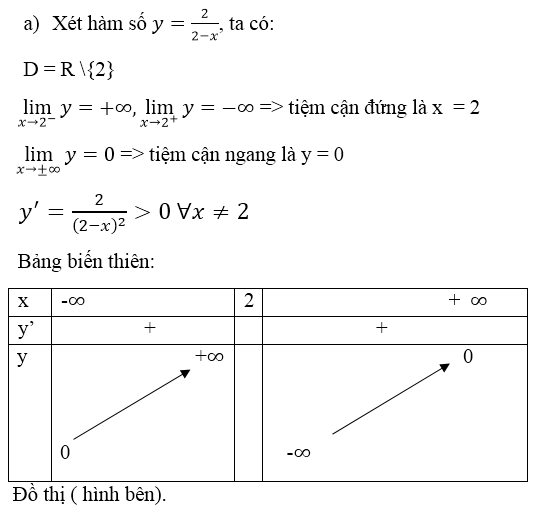
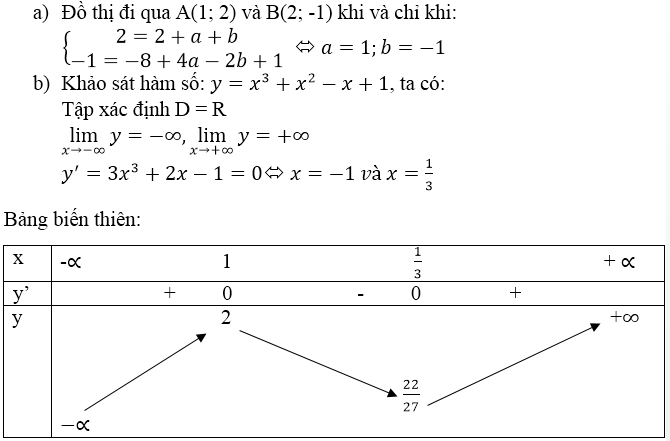
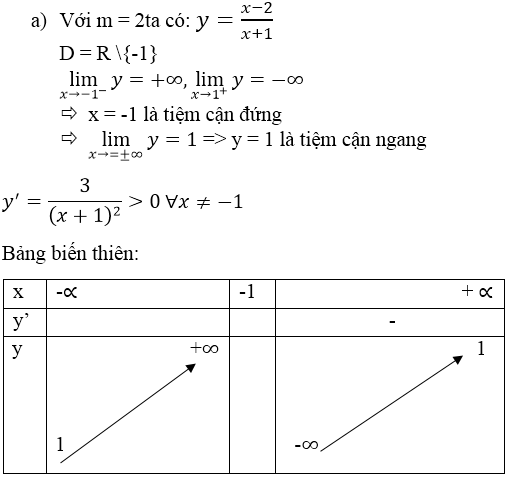
a) Học sinh tự giải
b) 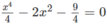
⇔ x 4 − 8 x 2 − 9 = 0
⇔ ( x 2 + 1)( x 2 − 9) = 0
⇔ 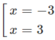
(C) cắt trục Ox tại x = -3 và x = 3
Ta có: y′ = x 3 − 4x
Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 3 và x = -3 lần lượt là:
y = y′(3)(x – 3) và y = y′(−3)(x + 3)
Hay y = 15(x – 3) và y = −15(x + 3)
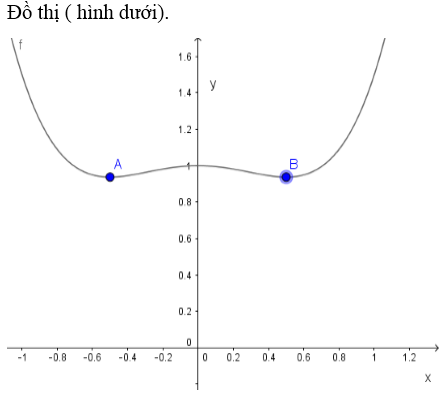
c) 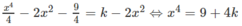
Từ đó, ta có:
k = −9/4: (C) và (P) có một điểm chung là (0; −9/4)
k > −9/4: (C) và (P) có hai giao điểm.
k < −9/4: (C) và (P) không cắt nhau.

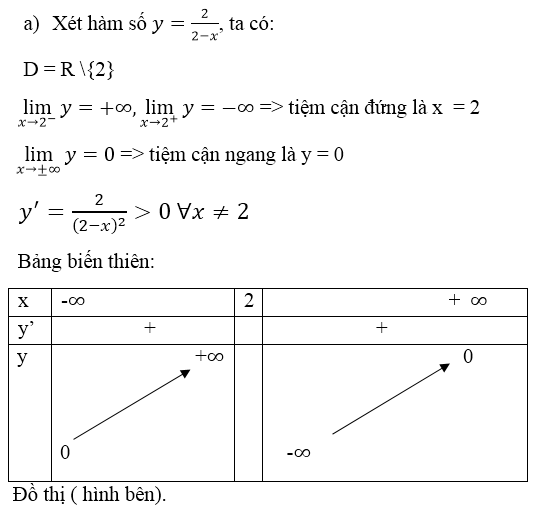
a) Hoành độ giao điểm của đồ thị hàm số \(y=\dfrac{2x+1}{2x-1}\) và \(y=x+2\) là nghiệm của phương trình :
\(\dfrac{2x+1}{2x-1}=x+2\Leftrightarrow\dfrac{2x+1}{2x-1}-x-2=0\)
\(\Leftrightarrow\dfrac{-2x^2-x+3}{2x-1}=0\)\(\Leftrightarrow\left\{{}\begin{matrix}-2x^2-x+3=0\\x\ne\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Với \(x=1\) thì \(y=1+2=3;x=-\dfrac{3}{2}\) thì \(y=-\dfrac{3}{2}+2=\dfrac{1}{2}\)
Vậy tọa độ hai giao điểm là \(A\left(1;3\right),B\left(-\dfrac{3}{2};\dfrac{1}{2}\right)\)

b) Ta có \(y'=4x^3-4x;y\left(-2\right)=8;y'\left(-2\right)=-24\)
Phương trình tiếp tuyến phải tìm là :
\(y-y\left(-2\right)=y'\left(-1\right)\left(x+2\right)\)
\(\Leftrightarrow y-8=-24\left(x+2\right)\Leftrightarrow y=-24x-10\)


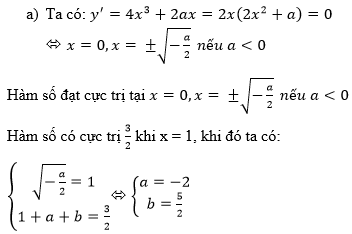

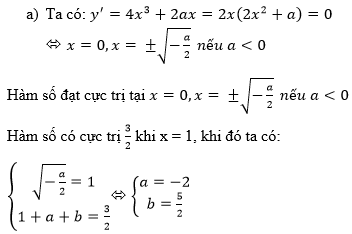
\(k>-\dfrac{9}{4}:\) (C) và (P) có hai giao điểm
\(k< -\dfrac{9}{4}:\) (C) và (P) không cắt nhau