Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) 
. Tập xác định : R 
{
} ;
và 
;
Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Tiệm cận đứng ∆ : x = .
A(-1 ;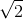 
) ∈ ∆ ⇔ = -1 ⇔ m = 2.
c) m = 2 =>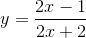 
.
a) . Tập xác định : R {} ;
và ;
Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Tiệm cận đứng ∆ : x = .
A(-1 ; 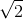) ∈ ∆ ⇔ = -1 ⇔ m = 2.
c) m = 2 => .
Đáp số M(1;0) 
Ai chỉ giúp em cách làm với ạ 
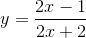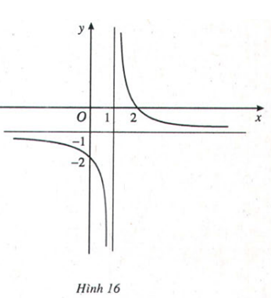
Từ đồ thị hàm số (H), để có hình (H’) nhận y = 2 là tiệm cận ngang và x = 2 là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị, sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương ứng sau:
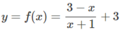
\(y'=4x\left(x-m\right)\left(x+m\right)\\ y'=0\Leftrightarrow\begin{cases}x=0\\x=\pm m\end{cases}\)
Với m=0 thì hàm số có 3 cực trị là 0, -m và m
đồ thị hàm số có 3 điểm cực trị \(A\left(0;1\right),M\left(-m;1-m^4\right),N\left(m;1-m^4\right)\)
Nhận thấy \(AM=AN\) nên \(\Delta AMN\) cân tại A với mọi m
Gọi trung điểm MN là \(I\left(0;1-m^4\right)\)
\(\Delta AMN\) vuông cân tại A khi và chỉ khi \(IA=IM=IN\) hay\(IA=IN\)
\(\Leftrightarrow IA=IN\Leftrightarrow\left|m^4\right|=\left|m\right|\Leftrightarrow m=\pm1\) (vì \(m\ne0\))
Lời giải:
PT hoành độ giao điểm:
\(mx+2m+1-\frac{2x+1}{x+1}=0\Leftrightarrow mx^2+x(3m-1)+2m=0\)
Để hai ĐTHS cắt nhau tại hai điểm $A,B$ thì \(m\neq 0\) và:
\(\Delta=(3m-1)^2-8m^2=m^2-6m+1>0\)
Khi đó áp dụng hệ thức Viete có \(\left\{\begin{matrix} x_1+x_2=\frac{1-3m}{m}\\ x_1x_2=2\end{matrix}\right.\)
Ta có:
\(d(A,Ox)=d(B,Ox)\Leftrightarrow |mx_1+2m+1|=|mx_2+2m+1|\)
TH1: \(mx_1+2m+1=mx_2+2m+1\Leftrightarrow x_1=x_2\)
\(\Rightarrow x_1=x_2=\sqrt{2}\Rightarrow \frac{1-3m}{m}=2\sqrt{2}\) kéo theo \(m=\frac{1}{2\sqrt{2}+3}\) (không thỏa mãn đk của \(\Delta)\)
TH2: \(mx_1+2m+1=-(mx_2+2m+1)\Leftrightarrow m(x_1+x_2)+4m+2=0\)
\(\Leftrightarrow 3+m=0\Rightarrow m=-3\) (t/m)
Vậy $m=-3$
😾
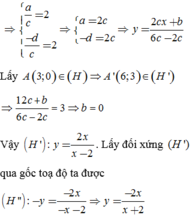