PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
1
NM
Nguyễn Minh Quang
Giáo viên
10 tháng 1 2022
ta có
\(y'=3x^2-6x=3x\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
y' >0 khi \(x\in\left(-\infty,0\right)\cup\left(2,+\infty\right)\)
Vậy hàm đồng biến trên hai khoảng là \(\left(-\infty,0\right)\cup\left(2,+\infty\right)\)
TT
1
17 tháng 12 2016
Điểm cực tiểu A(0;-2), điểm cực đại B(2;2)
Mình không hiểu đề bài yêu cầu tìm đường thẳng đi qua điểm A và B, đi qua cả A và B hay là các tiếp tuyến tại A và B?
25 tháng 3 2016
a) Xét phương trình \(f'\left(x\right)=2x^2+2\left(\cos a-3\sin a\right)x-8\left(1+\cos2a\right)=0\)
Ta có \(\Delta'=\left(\cos a-3\sin a\right)^2+16\left(1+\cos a\right)=\left(\cos a-3\sin a\right)^2+32\cos^2a\ge0\) với mọi a
Nếu \(\Delta'=0\Leftrightarrow\cos a-3\sin a=\cos a=0\Leftrightarrow\sin a=\cos a\Rightarrow\sin^2a+\cos^2a=0\) (Vô lĩ)
Vậy \(\Delta'>0\Rightarrow f'\left(x\right)=0\) có 2 nghiệm \(x_1,x_2\) và hàm số có cực đại và cực tiểu
b) Theo Viet ta có \(x_1+x_2=3\sin a-\cos a;x_1x_2=-4\left(1+\cos2a\right)\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(3\sin a-\cos a\right)^2+8\left(1+\cos2a\right)\)
\(=9+8\cos^2a-6\sin a\cos a\)
\(=9+9\left(\sin^2a+\cos^2a\right)-\left(3\sin a+\cos a\right)^2\)
\(=18-\left(3\sin a+\cos a\right)^2\le18\)
Q
31 tháng 3 2017
1. a) Tập xác định : D = R; y' = 3 - 2x => y' = 0 ⇔ x = \(\dfrac{3}{2}\).
Bảng biến thiên :
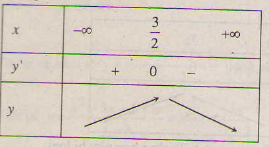
Hàm số đồng biến trên khoảng (-∞; \(\dfrac{3}{2}\)); nghịch biến trên khoảng ( \(\dfrac{3}{2}\); +∞ ).
b) Tập xác định D = R;
y'= x2 + 6x - 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên :
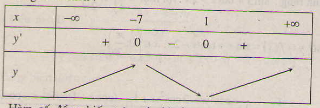
Hàm số đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).
c) Tập xác định : D = R.
y' = 4x3 - 4x = 4x(x2 - 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: tự vẽ.
Hàm số đồng biến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).
d) Tập xác định : D = R. y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = \(\dfrac{2}{3}\).
Bảng biến thiên :
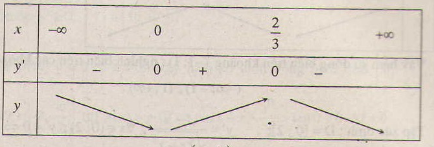
Hàm số đồng biến trên khoảng ( 0 ; \(\dfrac{2}{3}\) ) ; nghịch biến trên các khoảng (-∞ ; 0), ( \(\dfrac{2}{3}\); +∞).
31 tháng 3 2017
1. a) Tập xác định : D = R; y' = 3 - 2x => y' = 0 ⇔ x = \(\dfrac{3}{2}\).
Bảng biến thiên :
Hàm số đồng biến trên khoảng (-∞; \(\dfrac{3}{2}\)); nghịch biến trên khoảng ( \(\dfrac{3}{2}\); +∞ ).
b) Tập xác định D = R;
y'= x2 + 6x - 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên :
Hàm số đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).
c) Tập xác định : D = R.
y' = 4x3 - 4x = 4x(x2 - 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: tự vẽ.
Hàm số đồng biến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).
d) Tập xác định : D = R. y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = 2323.
Bảng biến thiên :
Hàm số đồng biến trên khoảng ( 0 ; \(\dfrac{2}{3}\) ) ; nghịch biến trên các khoảng (-∞ ; 0), ( \(\dfrac{2}{3}\); +∞).
LM
0
29 tháng 11 2022
Câu 1:
\(y=2\cdot\left(\dfrac{1}{2}sinx-cos\cdot\dfrac{\sqrt{3}}{2}\right)=2\cdot sin\left(x-\dfrac{pi}{3}\right)\)
=>-2<=y<=2
y=2 khi x-pi/3=pi/2+k2pi
=>x=5/6pi+k2pi
Đề thiếu rồi em