Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Từ đồ thị hàm số g = f’(x) ta thấy: hàm số f’(x) = 0 tại 2 điểm phân biệt x = -2 và x = 1
Mặt khác, tại x = 1 thì f’(x) đổi dấu từ dương sang âm, do đó hàm số y = f(x) đạt cực đại tại x = 1

a) y = f(x) = x3 – 3mx2 + 3(2m-1)x + 1
Tập xác định: D = R
y’= 3x2 -6mx + 3(2m-1) = 3(x2 – 2mx + 2m – 1)
Hàm số đồng biến trên D = R ⇔ y’ ≥ 0, ∀x ∈ R
⇔ x2 – 2mx + 2m - 1≥0, ∀x ∈ R
⇔ Δ’ = m2 – 2m + 1 = (m-1)2 ≤ 0 ⇔ m =1
b) Hàm số có một cực đại và một cực tiểu
⇔ phương trình y’= 0 có hai nghiệm phân biệt
⇔ (m-1)2 > 0 ⇔ m≠1
c) f’’(x) = 6x – 6m > 6x
⇔ -6m > 0 ⇔ m < 0

Chọn B
Để g( x) = f( x+ 1) => g’(x) = f’( x+1)
Hàm số y= g’(x) = f’( x+ 1) có đồ thị là phép tịnh tiến của đồ thị hàm số y= f’(x) theo phương trục hoành sang trái 1 đơn vị.
Khi đó đồ thị hàm số y= g’(x)= f’( x+1) vẫn cắt trục hoành tại 1 điểm.

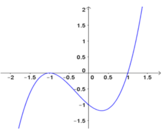
Dựa vào đồ thị ta thấy phương trình ![]() chỉ có một nghiệm đơn và hai nghiệm kép nên
chỉ có một nghiệm đơn và hai nghiệm kép nên ![]() chỉ đổi dấu khi qua nghiệm đơn này.
chỉ đổi dấu khi qua nghiệm đơn này.
Do đó suy ra hàm số f(x) có đúng một cực trị.
Chọn A.

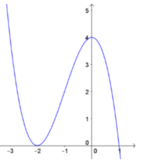
Dựa vào đồ thị ta thấy phương trình ![]() có ba nghiệm đơn và
có ba nghiệm đơn và ![]() đổi dấu khi qua nghiệm đơn này.
đổi dấu khi qua nghiệm đơn này.
Do đó suy ra hàm số ![]() có ba điểm cực trị.
có ba điểm cực trị.
Chọn C.

Chọn D
Phương pháp:
Từ đồ thị hàm số của f'(x) ta lập bảng biến thiên, từ đó xác định điểm cực trị của hàm số.
Hoặc ta sử dụng cách đọc đồ thị hàm số f'(x)
Số giao điểm của đồ thị hàm số f'(x) với trục hoành bằng số điểm cực trị của hàm số f'(x). (không tính các điểm tiếp xúc)
Nếu tính từ trái sang phải đồ thị hàm số f''=(x) cắt trục hoành theo chiều từ trên xuống thì đó là điểm cực đại của hàm số f(x).
Nếu tính từ trái sang phải đồ thị hàm số f'(x) cắt trục hoành theo chiều từ trên xuống thì đó là điểm cực tiểu của hàm số f(x).
Cách giải:
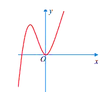
Từ đồ thị hàm số f'(x) ta thấy có một giao điểm với trục hoành (không tính điểm tiếp xúc) nên hàm số f(x) có một cực trị.

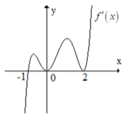
Đáp án B
Từ hình vẽ ta thấy, hàm số f'(x) = 0 có 2 nghiệm phân biệt x = 1 và x = -1.9x
Trong đó chỉ có tại x = 1 thì f'(x) đổi dấu từ âm sang dương, do đó hàm số y = f(x) có một điểm cực trị.