Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
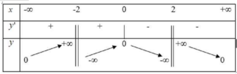
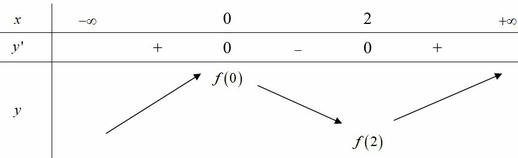
Phương pháp: Dựa vào bảng biến thiên để xác định tiệm cận, cực trị, giá trị lớn nhất, giá trị nhỏ nhất.
Cách giải: Dựa vào bảng biến thiên dễ thấy đồ thị hàm số có tiệm cận ngang y = 0 và hai tiệm cận đứng x = 2, x = -2. Vậy (I) sai và (IV) đúng.
Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
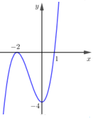
(I) sai. Ví dụ hàm số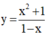 
có đồ thị hàm số như sau:
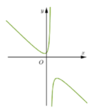õ ràng 
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số 
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: 
luôn song song với trục hoành.
Vậy (III) đúng.
hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
Chọn B.
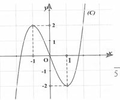
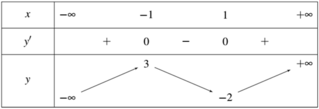
Cách 1: Số điểm cực trị của đồ thị hàm số y=|f(x)| bằng số điểm cực trị của đồ thị hàm số y=f(x) cộng với số giao điểm của đồ thị hàm số y=f(x)với trục hoành (không tính điểm cực trị)
Vì đồ thị hàm số y=f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm nên đồ thị hàm số y=|f(x)| có 2 + 1 = 3 điểm cực trị
Đáp án: 3 cực trị
Chọn A.
(I) sai f xđ trên R
(II) sai hs có 2 điểm cực trị
(III) ,(IV) đúng
Đáp án B
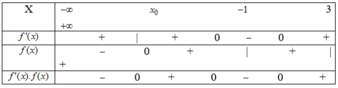
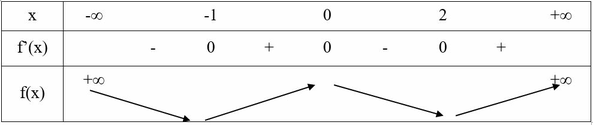
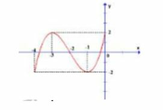
Dựa vào đồ thị hàm số f ' ( x ) ta thấy f ' ( x ) đổi dấu từ âm sang dương khi qua điểm x = 1 nên x = 1 là điểm cực tiểu của hàm số f ( x )
f ' ( x ) không đổi dấu khi đi qua điểm x = -2 nên x = -2 không phải điểm cực trị
Đáp án B
Dựa vào đồ thị hàm số f ' ( x ) ta thấy f ' ( x ) đổi dấu từ âm sang dương khi qua điểm x = 1 nên x = 1 là điểm cực tiểu của hàm số f ( x )
f ' ( x ) không đổi dấu khi đi qua điểm x = -2 nên x = -2 không phải điểm cực trị
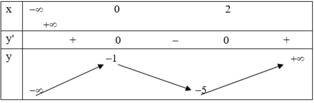
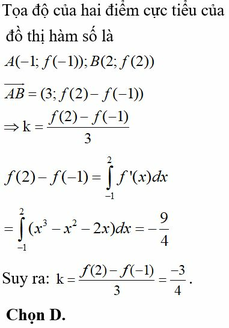
Đáp án đúng : C