Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(m^2-2m+1+2=\left(m-1\right)^2+2>0\left(\forall m\right)\)
\(x^2\ge0\left(\forall x\right)\)
\(\Rightarrow\left(m^2-2m+3\right)x^2\ge0\)
\(\Rightarrow f\left(\sqrt{2}\right)< f\left(\sqrt{5}\right)\)
Ta có : \(m^2-2m+3=m^2-2m+1+2\)
\(=\left(m-1\right)^2+2\ge2\) \(\left(Do\left(m-1\right)^2>0\right)\)
Nên khi x > 0 thì hàm số trên đồng biến.
Do \(\sqrt{2}< \sqrt{5}\Leftrightarrow f\left(\sqrt{2}\right)< f\left(\sqrt{5}\right)\)

Ta có \(4m-m^2-5=-\left(m-2\right)^2-1< 0\) \(\forall m\)
\(\Rightarrow f\left(x\right)\) nghịch biến trên R \(\Rightarrow f\left(a\right)>f\left(b\right)\Leftrightarrow a< b\)
Mà \(2-\sqrt{2019}>2-\sqrt{2020}\Rightarrow f\left(2-\sqrt{2019}\right)< f\left(2-\sqrt{2020}\right)\)

a) Vẽ đồ thị hàm số y = x2.
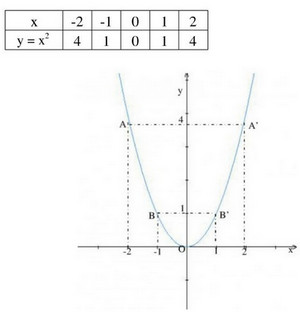
b) Ta có y = f(x) = x2 nên
f(-8) = (-8)2 = 64; f(-1,3) = (-1,3)2 = 1,69; f(-0,75) = (-0,75)2 = 0,5625; f(1,5) = 1,52 = 2,25.
c) Theo đồ thị ta có:
(0,5)2 ≈ 0,25
(-1,5)2 ≈ 2,25
(2,5)2 ≈ 6,25
d) Theo đồ thị ta có: Điểm trên trục hoành √3 thì có tung độ là y = (√3)2 = 3. Suy ra điểm biểu diễn √3 trên trục hoành bằng 1,7. Tương tự điểm biểu diễn √7 gồm bằng 2,7.

\(a=m^2-2m+3=\left(m-1\right)^2+2>0\) \(\forall m\)
\(\Rightarrow\) Hàm số đồng biến khi \(x>0\)
Vậy \(x_1>x_2>0\Rightarrow f\left(x_1\right)>f\left(x_2\right)\)
Mà \(\sqrt{5}>\sqrt{2}>0\Rightarrow f\left(\sqrt{5}\right)>f\left(\sqrt{2}\right)\)