Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét \(M\left(m;1+\frac{5}{m-3}\right)\) thuộc đồ thị đã cho
Theo yêu cầu bài tài <=> \(\left|m-3\right|=\left|\frac{5}{m-3}\right|\Leftrightarrow m=3\pm\sqrt{5}\)
Vậy \(M\left(3\pm\sqrt{5};1\pm\sqrt{5}\right)\)
Vì tam giác IAB cân tại I nên tiếp tuyến phải song song với một trong 2 đường thẳng có phương trình \(y=x;y=-x\).
Ta có \(y'=\frac{1}{\left(x+2\right)^2}>0;x\ne-2\)
Mọi \(M\left(x_0;y_0\right)\) là tiếp điểm thì \(y'\left(x_0\right)=1\Leftrightarrow1=\frac{1}{\left(x_0+2\right)^2}\Leftrightarrow\left[\begin{array}{nghiempt}x_0=-1\\x_0=-3\end{array}\right.\)
Từ đó suy ra 2 tiếp tuyến là \(y=x+1;y=x+5\)
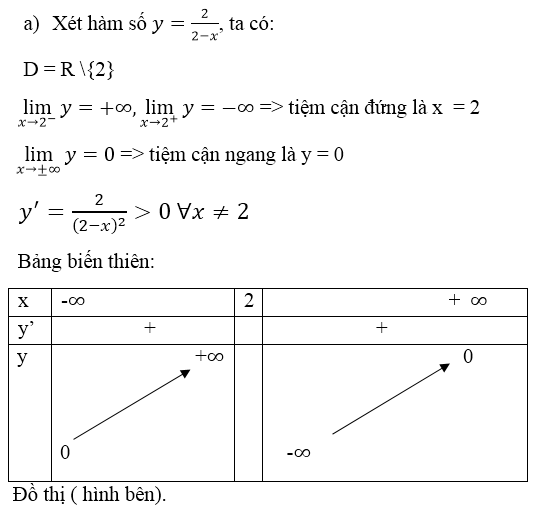
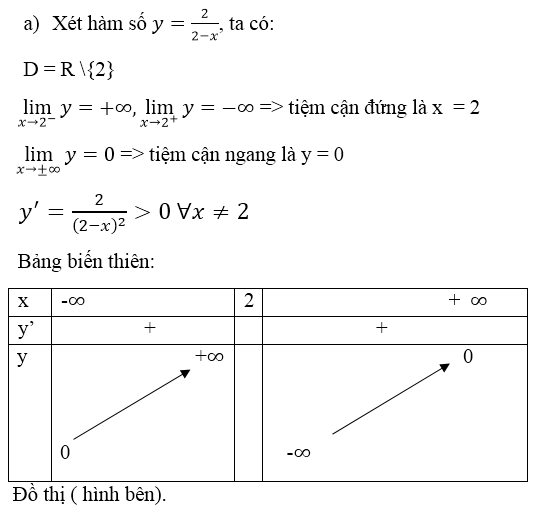
b) Tiệm cận đứng là đường thẳng \(x=3\)
Tiệm cận ngang là đường thẳng \(y=1\)
. Tập xác định : R 
{
} ;
và 
;
) ∈ ∆ ⇔ 
. 
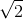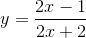Đáp án B