Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
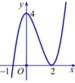
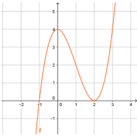
Từ đồ thị hàm số y = f(x) ta có trên khoảng (-1;3) có hai điểm cực trị.

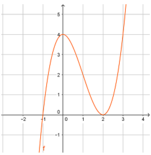
+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |

a) vẽ dễ lắm ; tự vẽ nha
b) xét phương trình hoành độ của 2 đồ thị đó
ta có : \(x^2=-2x+3\Leftrightarrow x^2+2x-3=0\)
ta có : \(a+b+c=1+2-3=0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=1\) \(\Rightarrow y=x^2=1^2=1\) vậy \(A\left(1;1\right)\)
\(x_2=\dfrac{c}{a}=-3\) \(\Rightarrow y=x^2=\left(-3\right)^2=9\) vậy \(B\left(-3;9\right)\)
vậy 2 đồ thị cắt nhau tại 2 điểm phân biệt là \(A\left(1;1\right)\) và \(B\left(-3;9\right)\)

Chọn B.
Phương pháp:
Dựa vào đồ thị hàm số xác định số điểm cực trị của hàm số.
Cách giải:
Đồ thị hàm số y = f(x) có 2 điểm cực trị.

Đáp án là B
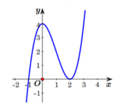
Nhìn vào đồ thị trên ta thấy đồ thị hàm số có điểm cực đại có tọa độ (0;4) và điểm cực tiểu có tọa độ (2;0), nên đồ thị hàm số trên có 2 điểm cực trị.
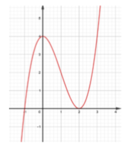
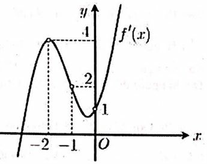


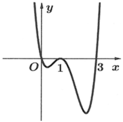

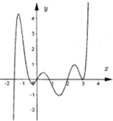

Đáp án A
Trên khoảng (-1;3) đồ thị hàm số có 2điểm cực trị là (0;4) và (2;0)