Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
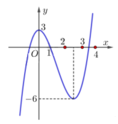
Kí hiệu trên đồ thị như hình bên.
Đặt u = f x . Ta có g x = f f x = f u .
g
'
x
=
u
'
.
f
'
u
=
f
'
x
.
f
'
u
g
'
x
=
0
⇔
f
'
x
=
0
f
'
u
=
0
f ' x = 0 ⇔ x 1 = 0 x 2 = a 2 < a < 3 (nhìn hình để xác định a).
f
'
u
=
0
⇔
u
=
x
1
u
=
x
2
⇔
f
x
=
x
1
=
0
f
x
=
x
2
=
a
2
<
a
<
3
f
x
=
0
⇔
x
∈
b
;
1
;
c
=
x
3
;
x
4
;
x
5
f x = a (nhìn vào đồ thị thể hiện bên ta thấy đồ thị hàm số f x cắt đường thẳng y = a (với 2 < a < 3 ) tại ba điểm phân biệt do vậy phương trình f x = a có ba nghiệm phân biệt x 6 ; x 7 ; x 8 .
Rõ ràng x 1 ,..., x 8 là đôi một khác nhau.
Kết hợp lại thì phương trình g ' x = 0 có 8 nghiệm phân biệt.

a: \(F\left(x\right)=x^4+6x^3+2x^2+x-7\)
\(G\left(x\right)=-4x^4-6x^3+2x^2-x+6\)
b: h(x)=f(x)+g(x)
\(=x^4+6x^3+2x^2+x-7-4x^4-6x^3+2x^2-x+6\)
\(=-3x^4+4x^2-1\)
c: Đặt h(x)=0
\(\Leftrightarrow3x^4-4x^2+1=0\)
\(\Leftrightarrow\left(3x^2-1\right)\left(x^2-1\right)=0\)
hay \(x\in\left\{1;-1;\dfrac{\sqrt{3}}{3};-\dfrac{\sqrt{3}}{3}\right\}\)

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k

b: Thay x=2 vào (P), ta được:
\(y=-\dfrac{1}{4}\cdot2^2=-1\)
Vì (d) đi qua O(0;0) và A(2;-1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0+b=0\\2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=0\end{matrix}\right.\)

a) vẽ dễ lắm ; tự vẽ nha
b) xét phương trình hoành độ của 2 đồ thị đó
ta có : \(x^2=-2x+3\Leftrightarrow x^2+2x-3=0\)
ta có : \(a+b+c=1+2-3=0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=1\) \(\Rightarrow y=x^2=1^2=1\) vậy \(A\left(1;1\right)\)
\(x_2=\dfrac{c}{a}=-3\) \(\Rightarrow y=x^2=\left(-3\right)^2=9\) vậy \(B\left(-3;9\right)\)
vậy 2 đồ thị cắt nhau tại 2 điểm phân biệt là \(A\left(1;1\right)\) và \(B\left(-3;9\right)\)




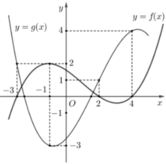

Đáp án B