Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hàm số : \(y=f\left(x\right)=\dfrac{2}{3}x+5\) với \(x\in R\)
Giả sử : \(x_1< x_2\)
\(f\left(x_1\right)=\dfrac{2}{3}x_1+5\)
\(f\left(x_2\right)=\dfrac{2}{3}x_2+5\)
Từ \(x_1< x_2\) \(\Rightarrow\dfrac{2}{3}x_1< \dfrac{2}{3}x_2\)
\(\Rightarrow\dfrac{2}{3}x_1+5< \dfrac{2}{3}x_2+5\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Vậy hàm số đồng biến trên \(R\)

Với x 1 , x 2 là hai giá trị bất kì của x thuộc R, ta có:
y 1 = f( x 1 ) = 4 - 2/5 x 1 ; y 2 = f( x 2 ) = 4 - 2/5 x 2
Nếu x 1 < x 2 thì x 1 - x 2 < 0. Khi đó ta có:
y 1 - y 2 = (4 - 2/5 x 1 ) - (4 - 2/5 x 2 )
= (-2)/5( x 1 - x 2 ) > 0. Suy ra y 1 > y 2
Vậy hàm số đã cho là hàm nghịch biến trên R.

\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{3x_1-2-3x_2+2}{x_1-x_2}=3\)
Vậy: Hàm số đồng biến trên R

hàm số đồng biến khi x tăng thì y tăng
ta xét với mọi \(x_1< x_2\) ta có :
\(\Rightarrow y_1=2x_1-3< 2x_2-3=y_2\)
vậy hàm số đã cho đồng biến trên R
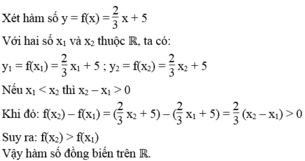


y = ( a 2 - 2a + 4)x - 9
Ta có: a 2 - 2a + 4 = a 2 - 2a + 1 + 3 = a - 1 2 + 3 > 0 ∀a
Vậy hàm số luôn đồng biến trên R