Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a: khi m= 2 => y=2x+2
y y=2x+2 x -1 2 0
với x=0=> y =2
với y=0 =>x -1
câu b : y = xm+2 cắt ox,oy lần lượt tại A,B mà tam giác OAB cân tại O nên OB=OA \(OA^2=OB^2\)
Y X 0 A B
Với x=0=>y=2 => A(0,2) => \(0A=\sqrt{0^2+2^2}=2\)
Với y=0=> x= \(x=\frac{-2}{m}\)nên \(B\left(\frac{-2}{m},0\right)\) ,\(OB=\sqrt{\frac{4}{m^2}+0^2}=\sqrt{\frac{4}{m^2}}\)
theo giả thiết OA=OB nên \(\sqrt{\frac{4}{m^2}}=\sqrt{4}\Leftrightarrow m^2=1\Leftrightarrow\orbr{\begin{cases}m=1\\m=-1\end{cases}}\)

4) Cùng cắt nhau tại 1 điểm trên trục tung nên x = 0 => m - 3 = 5 => m = 8
3) \(m=\frac{2+\sqrt{2}}{2\sqrt{2}-1}=\frac{\left(2+\sqrt{2}\right)\left(2\sqrt{2}+1\right)}{7}=\frac{5\sqrt{2}+6}{7}\)

a) Hàm số nghịch biến trên R <=> a < 0
<=> 2m - 1 < 0
<=> 2m < 1
<=> m < 1/2
b) Gọi điểm bị cắt là A ( x;y )
cắt trục hoành tại điểm có tọa độ -1
=> x = -1 ; y = 0
=> A ( -1 ; 0 )
Ta có y = ( 2m - 1)x + m - 1 cắt A ( -1;0 )
=> 0 = ( 2m -1 ). ( -1 ) + m - 1
<=> -2m + 1 + m - 1 =0
<=> -m = 0
<=> m = 0
Vậy khi m = 0 thì đồ thị của hàm số cắt trục hoành tại điểm có hoành độ -1
c) y x 0 1 4 M ( 1;4 ) y=(2m............ -1 E F H
Vì đồ thị của hàm số ( đtchs ) đi qua M(1;4) nên thay điểm M vào đtchs ta được:
4 = ( 2m - 1).1+m - 1
<=> 4 = 2m - 1 + m - 1
<=> 4 = 3m - 2
<=> 6 = 3m
<=> m = 2 ( 1 )
Gọi \(E\left(x_E;y_E\right)\)là điểm nằm trên trục tung vào được đtchs đi qua
Và ta có \(x_E=0\) ( vì xE trùng với góc tọa độ ) ( 2 )
Thay ( 1 ) và ( 2 ) vào đtchs ta được:
y = ( 2 . 2 - 1 ). 0 + 2 - 1
y = 2 - 1
y = 1
Áp dụng hệ thức lượng vào tam giác OEF vuông tại O
\(\frac{1}{OH^2}=\frac{1}{OE^2}+\frac{1}{OF^2}\)
\(\Leftrightarrow\frac{1}{OH^2}=\frac{1}{1^2}+\frac{1}{\left(-1\right)^2}\)
\(\Leftrightarrow\frac{1}{OH^2}=2\)
\(\Leftrightarrow2OH^2=1\)
\(\Leftrightarrow OH^2=\frac{1}{2}\)
\(\Leftrightarrow\orbr{\begin{cases}OH=\frac{\sqrt{2}}{2}\left(nhận\right)\\OH=-\frac{\sqrt{2}}{2}\left(loại\right)\end{cases}}\) ( loại -v2/2 vì độ dài không có giá trị âm )
Vậy khoảng cách từ gốc tọa độ O đến đường thẳng đó là \(\frac{\sqrt{2}}{2}\)
HỌC TỐT !!!!
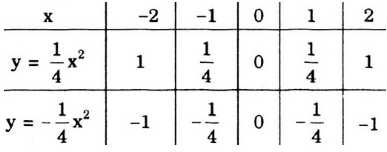
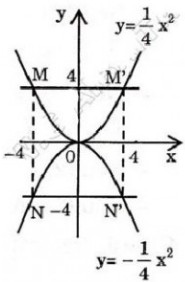

\(y=\left(2m-1\right)x+m+1\left(m\ne\dfrac{1}{2}\right)\)
\(x=0\Rightarrow y=m+1\Rightarrow A\left(0;m+1\right)\Rightarrow OA=\left|m+1\right|\)
\(y=0\Rightarrow x=\dfrac{-m-1}{2m-1}=\dfrac{m+1}{1-2m}\Rightarrow B\left(\dfrac{m+1}{1-2m};0\right)\Rightarrow OB=\left|\dfrac{m+1}{1-2m}\right|\)
\(\Delta OAB-cân-tạiO\Leftrightarrow OA=OB>0\Rightarrow\left\{{}\begin{matrix}\left|m+1\right|>0\\\left|\dfrac{m+1}{1-2m}\right|>0\end{matrix}\right.\)\(\Leftrightarrow-1< m< \dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}m+1=\dfrac{m+1}{1-2m}\\m+1=\dfrac{-\left(m+1\right)}{1-2m}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m=-1\left(ktm\right);m=0\left(tm\right)\\m=1\left(tm\right);m=-1\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)
PT giao Ox và Oy:
\(\left\{{}\begin{matrix}y=0\Rightarrow\left(2m-1\right)x=-\left(m+1\right)\Rightarrow x=\dfrac{m+1}{1-2m}\Rightarrow A\left(\dfrac{m+1}{1-2m};0\right)\Rightarrow OA=\left|\dfrac{m+1}{1-2m}\right|\\x=0\Rightarrow y=m+1\Rightarrow B\left(0;m+1\right)\Rightarrow OB=\left|m+1\right|\end{matrix}\right.\)
\(\Delta AOB\text{ cân}\\ \Leftrightarrow OA=OB\Leftrightarrow\left|\dfrac{m+1}{1-2m}\right|=\left|m+1\right|\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{m+1}{1-2m}=m+1\\\dfrac{m+1}{2m-1}=m+1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left(m+1\right)\left(1-2m\right)-\left(m+1\right)=0\\\left(m+1\right)\left(2m-1\right)-\left(m+1\right)=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}-2m\left(m+1\right)=0\\\left(m+1\right)\left(2m-2\right)=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=1\\m=-1\end{matrix}\right.\)