Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

với \(m=0\) : PT \(\left(1\right)\Leftrightarrow\) \(-2x+1=0\) \(\Leftrightarrow x=\frac{1}{2}\in\left(0;1\right)\)
với \(m\ne0\) : PT \(\left(1\right)\) có đúng 1 nghiệm \(\in\left(0;1\right)\)
\(\Leftrightarrow f\left(0\right).f\left(1\right)<0\)
( để ý: \(\Delta'=\left(m+1\right)^2-m=\)\(m^2+m+1>0,\text{∀}x\in R\))
\(\Leftrightarrow m-2\left(m+1\right)+1<0\) \(\Leftrightarrow m>-1\)
vậy \(m>-2\) là kết quả cần tìm
với m=0m=0 : PT (1)⇔(1)⇔ −2x+1=0−2x+1=0 ⇔x=12∈(0;1)⇔x=12∈(0;1)
với m≠0m≠0 : PT (1)(1) có đúng 1 nghiệm ∈(0;1)∈(0;1)
⇔f(0).f(1)<0⇔f(0).f(1)<0
( để ý: Δ′=(m+1)2−m=Δ′=(m+1)2−m=m2+m+1>0,∀x∈Rm2+m+1>0,∀x∈R)
⇔m−2(m+1)+1<0⇔m−2(m+1)+1<0 ⇔m>−1⇔m>−1
vậy m>−2m>−2 là kết quả cần tìm

Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k

Để x=1 là nghiệm của f(x)
thì a.13+b.12+c.1+d=0
<=>a+b+c+d=0
Vậy..........

a/ f(x) = 0 => x2 + 4x - 5 = 0 => (x - 1)(x + 5) = 0 => x = 1 hoặc x = -5
Vậy x = 1 , x = -5
b/ f(x) > 0 => x2 + 4x - 5 > 0 => (x - 1)(x + 5) > 0 => x - 1 > 0 và x + 5 > 0 => x > 1 và x > -5 => x > 1
hoặc x - 1 < 0 và x + 5 < 0 => x < 1 và x < -5 => x < -5
Vậy x > 1 hoặc x < -5
c/ f(x) < 0 => x2 + 4x - 5 < 0 => (x - 1)(x + 5) < 0 => x - 1 > 0 và x + 5 < 0 => x > 1 và x < -5 => vô lí
hoặc x - 1 < 0 và x + 5 > 0 => x < 1 và x > -5 => -5 < x < 1
Vậy -5 < x < 1

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
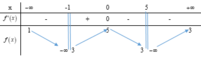


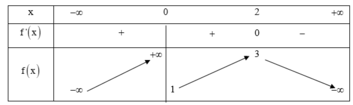
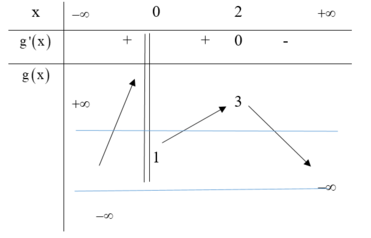
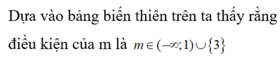
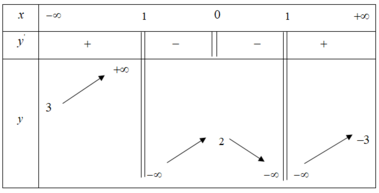

Phương pháp:
Biện luận số nghiệm của phương trình thông qua số giao điểm của hai đồ thị hàm số.