Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)

f(0)=2014=a.0^2+b.0+c=c => c=2014
f(1)=2015= a.1^2+b.1+c = a+b+c=a+b+2014 => a+b=2015-2014=1 (*)
f(-1)=2017=a.(-1)^2+b.(-1)+c= a-b+c=a-b+2014 =>a-b=2017-2014=3(**)
từ (*) và (**) ta có hệ pt và tính được a=2 và b= -1
=> f(-2) = 2.(-2)^2 + (-1).(-2) +2014=2024
F(0) = a.02 + b. 0 + c = 2014 => c = 2014
F(1) = a.12 + b. 1+ 2014 = 2015 => a + b = 2015 - 2014 = 1
F(-1) = a.(-1)2 + b.(-1) + 2014 = 2017 = > a - b = 2017 - 2014 = 3
Cộng vế cho vế ta được : 2a = 1 + 3 = 4=> a = 4/2 =2
thay a = 2 vào a + b = 1 ta có
2 + b = 1 => b = -1
F(x) = 2x2 - x + 2014
Vậy F(-2) = 2. (-2)2 - (-2) + 2014 = 2024

a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)

a: TXĐ: D=R
b: \(f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1\)
\(f\left(0\right)=\sqrt{0+1}=1\)
\(f\left(1\right)=\sqrt{1+1}=\sqrt{2}\)
\(f\left(2\right)=\sqrt{3}\)

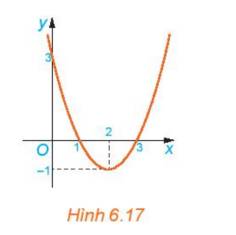
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a

Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)

Thấy f(x) = f [ (x-1) +1 ] = (x+1)^2 -3(x+1) + 3 = x^2 -x -2
Đặt \(x+1=t\Rightarrow x=t-1\)
\(f\left(t\right)=\left(t-1\right)^2-2\left(t-1\right)+3=t^2-2t+1-2t+2+3=t^2-4t+6\)
Vậy \(f\left(x\right)=x^2-4x+6\)