Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
.
.
.
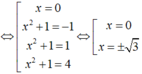
Các nghiệm trên đều là các nghiệm bội lẻ, do đó đều là cực trị của hàm số 
Xét x = -1 ta có 
từ đó ta có bảng xét dấu g’(x) như sau:
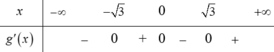
Dựa vào các đáp án ta thấy hàm số y = g(x) nghịch biến trên (0;1)
Chọn B
\(f\left(x\right)+g\left(x\right)=-x\left[f'\left(x\right)+g'\left(x\right)\right]\)
Đặt \(h\left(x\right)=f\left(x\right)+g\left(x\right)\Rightarrow\left\{{}\begin{matrix}h\left(1\right)=4\\h\left(x\right)=-x.h'\left(x\right)\end{matrix}\right.\)
\(\Rightarrow\frac{h'\left(x\right)}{h\left(x\right)}=-\frac{1}{x}\Rightarrow\int\frac{h'\left(x\right)}{h\left(x\right)}dx=-\int\frac{dx}{x}=-lnx\)
\(\Rightarrow ln\left[h\left(x\right)\right]=ln\left(\frac{1}{x}\right)+C\)
Thay \(x=1\Rightarrow C=ln4\Rightarrow ln\left[h\left(x\right)\right]=ln\left(\frac{1}{x}\right)+ln4=ln\left(\frac{4}{x}\right)\)
\(\Rightarrow h\left(x\right)=\frac{4}{x}\)
\(\Rightarrow I=\int\limits^4_1h\left(x\right)dx=\int\limits^4_1\frac{4}{x}dx=...\)
cho em hỏi tại sao h(x) =\(\frac{4}{x}\) mà ko phải là |h(x)| vậy ạ?
Bạn coi lại đề bài, có gì đó không ổn
Thay \(x=1\) vào \(g\left(x\right)=-x.f\left(x\right)\) \(\Rightarrow g\left(1\right)=-f\left(1\right)\)
\(\Rightarrow f\left(1\right)+g\left(1\right)=0\) trái với điều kiện \(f\left(1\right)+g\left(1\right)=4\)????
dạ em viết nhầm, phải là g(x)=-xf'(x) f(x)=-xg'(x) mới đúng
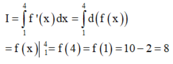
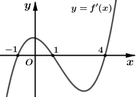
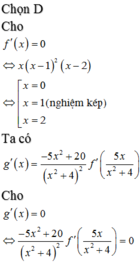
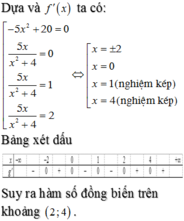
Đáp án B.