K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

3 tháng 4 2019
đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.
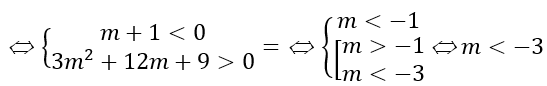
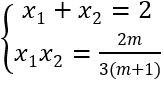
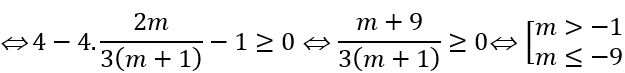
Ta có:
f(x) = x ( x- 1) \(\ge\)-1/4 với mọi x \(\in\)(0; 1]
+) f(x+1) = 2f(x) = 2x(x-1) với mọi x \(\in\)(0; 1]
=> f(x) = 2(x-1) (x- 2) với mọi x \(\in\)( 1; 2]
=> f(x) = 2(x-1) (x- 2) \(\ge\)-1/2 với mọi x \(\in\)( 1; 2]
+) f(x + 1 ) = 2 f(x) = 4 ( x - 1 ) ( x - 2 ) với x \(\in\)( 1; 2]
=> f (x ) = 4 ( x - 2 ) ( x - 3 ) với mọi x \(\in\)( 2; 4 ]
=> f (x ) = 4 ( x - 2 ) ( x - 3 ) \(\ge\)-1 với mọi x \(\in\)( 2; 3 ]
dấu bằng xảy ra tại x = 5/2 điểm cực tiểu
mà theo để ra tìm m để \(f\left(x\right)\ge-\frac{8}{9}\)với mọi x ( - \(\infty\); m ]
=>2< m < 5/2 và f(m) = -8/9
<=> m = 7/3
[URL=http://www.mediafire.com/view/corexjfrbst6qsw/f%2528x%252B1%2529.jpg/file][IMG]https://www.mediafire.com/convkey/6ebc/corexjfrbst6qsw4g.jpg[/IMG][/URL]
Em vẫn chưa hiểu phần trong khung đỏ , tại sao từ
f(x+1) = 2f(x) = 4(x-1)(x-2) với x thuộc [1.2]
ta lại suy ra được f(x) =4(x-2)(x-3) >= -1 với mọi x thuộc [2,3]
Thầy cô giải thích thêm giùm em được không ạ ,em cám ơn thầy cô nhiều