Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

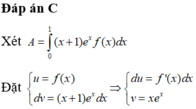
⇒ A = x e x f x 1 0 - ∫ 0 1 x e x f ' x d x = - ∫ 0 1 x e x f ' x d x = 1 - e 2 4
Xét ∫ 0 1 x 2 e 2 x d x = e 2 x 1 2 x 2 - 1 2 x + 1 4 1 0 = e 2 - 1 4
Ta có ∫ 0 1 f ' x 2 d x + 2 ∫ 0 1 x e x f ' x d x + ∫ 0 1 x 2 e 2 x f x d x = 0 ⇔ ∫ 0 1 f ' x + x . e x 2 d x = 0 f ' x + x . e x = 0 , ∀ x ∈ 0 ; 1 d o f ' x + x . e x 2 ≥ 0 , ∀ x ∈ 0 ; 1 ⇒ f ' x = - x e x ⇒ f x = 1 - x e x + C f 1 = 0 ⇒ f x = 1 - x e x ⇒ I = ∫ 0 1 f x d x = ∫ 0 1 1 - x e x d x = 2 - x e x 1 0 = e - 2
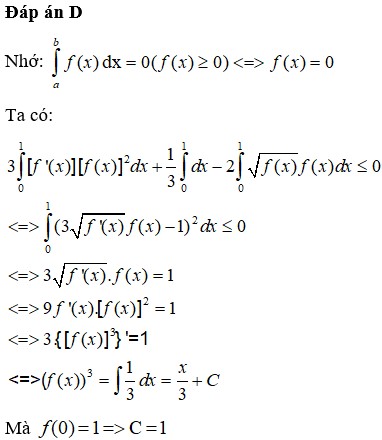
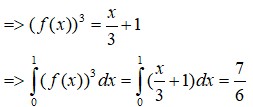
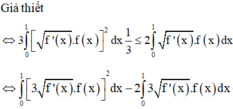

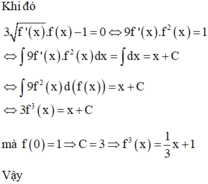

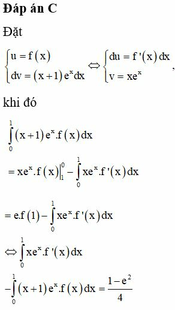
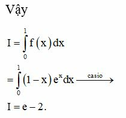
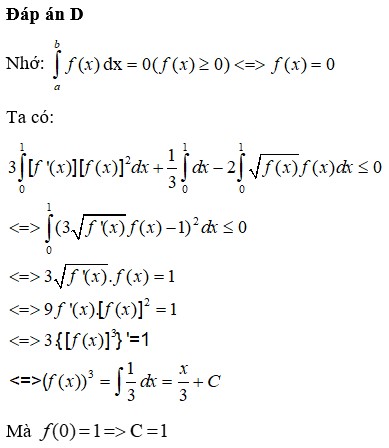
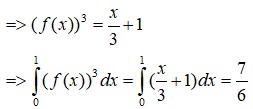


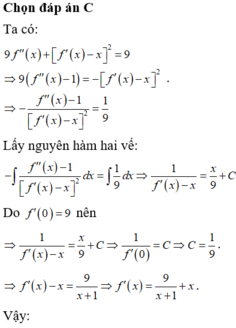
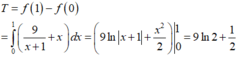
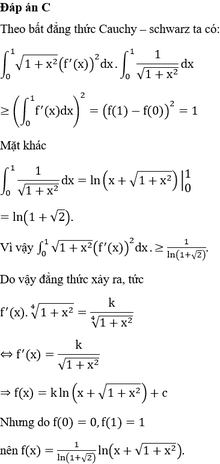
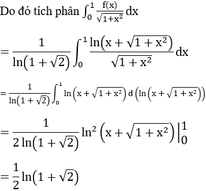
Đáp án C
⇒ f ' ( x ) + x e x = 0 , ∀ x ∈ [ 0 ; 1 ] ( d o f ' x + x e x 2 ≥ 0 , ∀ x ∈ [ 0 ; 1 ] ) ⇒ f ' ( x ) = − x e x ⇒ f ( x ) = ( 1 − x ) e x + C f ( 1 ) = 0 ⇒ f ( x ) = ( 1 − x ) e x ⇒ I = ∫ 0 1 f ( x ) d x = ∫ 0 1 ( 1 − x ) e x d x = ( 2 − x ) e x 1 0 = e − 2