K
Khách
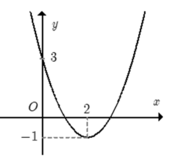
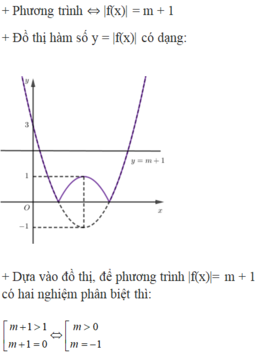
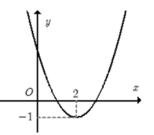
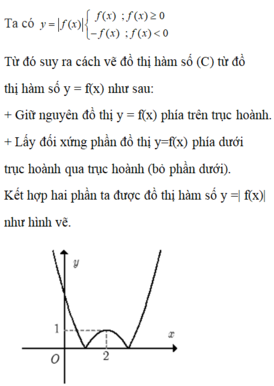
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
13 tháng 10 2020
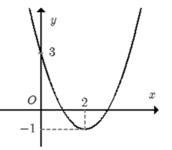
Đề là đồ thị có đỉnh là \(\left(1;2\right)\) thì hợp lí hơn
\(f\left(x\right)+m-2018=0\)
\(\Leftrightarrow f\left(x\right)=2018-m\) là phương trình hoành độ giao điểm của hai đồ thị \(y=m-2018;y=f\left(x\right)\)
Phương trình \(f\left(x\right)+m-2018=0\) có nghiệm duy nhất khi \(2018-m=2\Leftrightarrow m=2016\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 2 2020
\(\Delta=b^2-4ac\le0\Rightarrow b^2\le4ac\Rightarrow\frac{a}{b}.\frac{c}{b}\ge\frac{1}{4}\)
Đặt \(\left(\frac{a}{b};\frac{c}{b}\right)=\left(x;y\right)\Rightarrow xy\ge\frac{1}{4}\)
\(F=4x+y\ge4\sqrt{xy}\ge4\sqrt{\frac{1}{4}}=2\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x=\frac{1}{4}\\y=1\end{matrix}\right.\) hay \(b=c=4a\)