Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Muốn xác định được hệ số \(a\) ta thay \(x=1\) và \(y=2,5\) vào công thức \(y=ax+3\).
Ta có: \(y=ax+3\Leftrightarrow2,5=a.1+3\Leftrightarrow a=-3+2,5\Leftrightarrow a=-0,5\)

a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a.2 + 3.
Suy ra hệ số góc a = 3/2 và được hàm số y = 3/2x + 3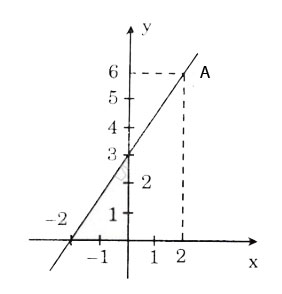
b) Hàm số đã cho là y = 3/2x + 3. Đồ thị được vẽ như hình bên.
Bài giải:
a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a . 2 + 3.
Suy ra hệ số góc a = 1, 5.
b) Hàm số đã cho là y = 1,5x + 3. Đồ thị được vẽ như hình bên.
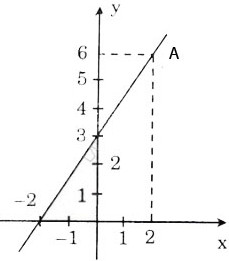

a) y = 1 - 5x là một hàm số bậc nhất với a = -5, b = 1. Đó là một hàm số nghịch biến vì -5 < 0.
b) y = -0,5x là một hàm bậc nhất với a \(\approx\)-0,5, b = 0. Đó là một hàm số nghịch biến vì -0,5 < 0.
c) y = \(\sqrt{ }\)2(x - 1) + \(\sqrt{ }\)3 là một hàm số bậc nhất với a = \(\sqrt{ }\)2, b = \(\sqrt{ }\)3 - \(\sqrt{ }\)2. Đó là một hàm số đồng biến vì \(\sqrt{ }\)2 > 0.
d) y = 2x2 + 3 không phải là một hàm số bậc nhất vì nó không có dạng y = ax + b, với a \(\ne\) 0.


Theo giả thiết 2,5 = a . 1 +3.
\(\Rightarrow\) a = 2,5 - 3 = -0,5.