Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ điều kiện đề bài: (hiển nhiên a khác 0):
\(\left\{{}\begin{matrix}\dfrac{4ac-b^2}{4a}=-1\\a-b+c=7\\c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a-b^2=-4a\\a-b=6\\c=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-6\right)^2-8a=0\\b=a-6\\c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\left\{2;18\right\}\\b=a-6\\c=1\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=2x^2-4x+1\\y=18x^2+12x+1\end{matrix}\right.\)

Với \(a\ne0\) từ đề bài ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a+b=0\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\)
\(\Rightarrow a=-1;b=4;c=-3\)
Vậy (P): \(y=-x^2+4x-3\)

- Từ các giả thiết của đề bài ta có hệ phương trình :
\(\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\-\dfrac{b}{2a}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{9}a+\dfrac{1}{3}b+c=-\dfrac{4}{3}\\4a+2b+c=7\\2a+3b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-2\\c=-1\end{matrix}\right.\)
Vậy hàm số trên có dạng : \(3x^2-2x-1=0\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-4x+1=2x-4\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+5=0\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-5\right)=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(1;-2\right);\left(5;6\right)\right\}\)
c: Điểm M,N ở đâu vậy bạn?

Vì đồ thị hàm số đi qua điểm A(-2;7) nên ta có:
4a-2b+c=7 (1)
Vì đồ thị hàm số đi qua điểm B(3;2) nên ta có:
4a+2b+c=2 (2)
Giá trị nhỏ nhất là -2 => \(\dfrac {-b^2+4ac}{4a}\)=-2
<=>-8a+\(b^2\)-4ac=0 (3) (a khác 0)
Lấy (1) trừ (2) ta có:
b= \(\dfrac {-5}{4}\) thay vào (1) ta có:
(1) 4a+\(\dfrac {5}{2}\)+c=7
<=>4a+c=4.5
<=> c=4.5-4a
thay b và c vừa tìm vào (3) ta có:
\(16a^2 \) -26a+\(\dfrac {25}{16}\) =0
=> a=25/16
hoặc a=1/16
=> c =13/4
hoặc a=37/4

Đáp án C
Từ giả thiết, ta có hệ:
− b 2 a = − 2 4 a − 2 b + c = 5 a + b + c = − 1 ⇔ a = − 2 3 ; b = − 8 3 ; c = 7 3
⇒ S = a 2 + b 2 + c 2 = 13
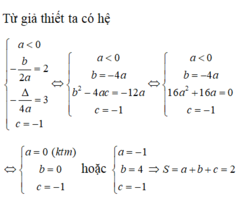


Lời giải:
Để hàm số có GTLN thì $a< 0$
Hàm số đạt giá trị lớn nhất tại \(x=\frac{-b}{2a}=1\Leftrightarrow -b=2a(1)\)
Hàm số đạt giá trị cực đại (giá trị lớn nhất) là \(f(1)=a+b+c=a^2+4(2)\)
ĐT hàm số đi qua điểm $(3,1)\Rightarrow 1=9a+3b+c(3)$
Từ \((1);(2);(3)\Rightarrow \left\{\begin{matrix} b=-2a\\ a+b+c=a^2+4\\ 9a+3b+c=1\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} b=-2a\\ a+(-2a)+c=a^2+4\\ 9a+3(-2a)+c=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=-2a\\ c=a^2+a+4\\ c=1-3a\end{matrix}\right.\)
\( \Rightarrow \left\{\begin{matrix} a=-1\\ b=2\\ c=4\end{matrix}\right.\) hoặc \( \left\{\begin{matrix} a=-3\\ b=6\\ c=10\end{matrix}\right.\)