
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B.
Phương pháp : Chuyển vế, lấy nguyên hàm hai vế.
Cách giải :
![]()
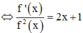
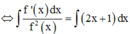
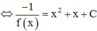
![]()
![]()
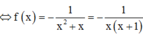
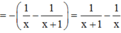
![]()
![]()
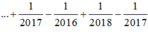
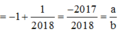
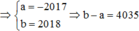

Đáp án B.
Cho m=1 ta có
f ( n + 1 ) = f ( n ) + f ( 1 ) + n ⇔ f ( n + 1 ) = f ( n ) + n + 1.
Khi đó
f ( 2 ) + f ( 3 ) + ... + f ( k ) = f ( 1 ) + 2 + f ( 2 ) + 3 + ... + f ( k − 1 ) + k + 1
⇔ f ( 2 ) + f ( 3 ) + ... + f ( k − 1 ) + f ( k ) = f ( 1 ) + f ( 2 ) + ... + f ( k − 1 ) + ( 1 + 2 + ... + k )
⇔ f ( k ) = f ( 1 ) + ( 1 + 2 + ... + k ) = 1 + k ( k + 1 ) 2 .
Vậy hàm cần tìm là
f ( x ) = 1 + x ( x + 1 ) 2 ⇒ f ( 96 ) = 1 + 96.97 2 = 4657 f ( 69 ) = 1 + 69.70 2 = 2416
Vậy
T = log 4657 − 2416 − 241 2 = log 1000 = 3.

Lời giải:
\(A=a_1a_2+a_2a_3+....+a_{n-1}a_n+a_na_1=0\)
Nếu $n$ lẻ, ta thấy tổng $A$ gồm lẻ số hạng, mỗi số hạng có giá trị $1$ hoặc $-1$ nên $A$ lẻ \(\Rightarrow A\neq 0\) (vô lý)
Do đó $n$ chẵn. Nếu $n$ có dạng $4k+2$. Vì $A=0$ nên trong $4k+2$ số hạng trên sẽ có $2k+1$ số có giá trị là $1$ và $2k+1$ số có giá trị $-1$. Vì mỗi số $a_i$ trong $A$ xuất hiện $2$ lần nên \(a_1a_2a_2a_3....a_{n-1}a_na_{n}a_{1}=(a_1a_2...a_n)^2=1^{2k+1}(-1)^{2k+1}=-1\) (vô lý)
Do đó $n$ phải có dạng $4k$, tức là $n$ chia hết cho $4$ (đpcm)

f ( 1 - x ) + x 2 f ' ' ( x ) = 2 x 1
Thay x=0 vào (1) ta được f(1)=0
Đạo hàm hai vế của (1) ta có - f ' ( 1 - x ) + 2 x f ' ' ( x ) + x 2 f ' ' ' ( x ) = 2 2
Thay x=0 vào (2) ta được f'(1)=2
Mặt khác, lấy tích phân hai vế cận từ 0 đến 1 của (1) ta có:
∫ 0 1 f ( 1 - x ) d x + ∫ 0 1 x 2 f ' ' ( x ) d x = ∫ 0 1 2 x d x
⇔ - ∫ 0 1 f ( 1 - x ) d ( 1 - x ) + f ' ( 1 ) - 2 ∫ 0 1 x f ' ( x ) d x = 1 ⇔ ∫ 0 1 f ( x ) d x - 2 ∫ 0 1 x f ' ( x ) d x = 3
Đặt ∫ 1 f ( x ) d x = I 1 . Vì
∫ 0 1 x f ' ( x ) d x = f ( 1 ) - ∫ 0 1 f ( x ) d x = - ∫ 0 1 f ( x ) d x
nên ta có hệ: I 1 - 2 I = 3 I = - I 1 ⇔ I 1 = 1 I = - 1
Vậy I=-1
Chọn đáp án B.