Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(2,y\right)=0\)
\(\Leftrightarrow\left(5.2-3y+3\right)\left(4.2+2y-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}13-3y=0\\7+2y=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}y=\frac{13}{3}\\y=-\frac{7}{2}\end{cases}}\).

A B C D
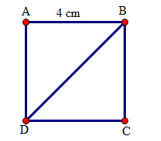
Gọi hình vuông ABCD có cạnh là 4 cm với đường chéo AD
có tam giác ACD vuông tại C
=> AC2+CD2=AD2 ( định lí Pitago)
42 .2=AD2
32=AD2
AD2=\(\sqrt{32}\)
Xét tam giác ABD vuông tại A, ta có:
BD2 = AB2 + AD2
BD2 = 42 + 42
BD2 = 16 + 16
BD2 = 32
BD = \(\sqrt{32}\)\(=4\sqrt{2}\left(cm\right)\)

\(8x^2+59x+66=8x^2+48x+11x+66\)
\(=8x\left(x+6\right)+11\left(x+6\right)=\left(8x+11\right)\left(x+6\right)\)
\(8x^2+59x+66=8x^2+48x+11x+66=8x\left(x+6\right)+11\left(x+6\right)\)
\(=\left(8x+11\right)\left(x+6\right)\)

Thay \(x=2\)
Ta có:\(6.2+m=3.2+3\)
\(\Leftrightarrow12+m=9\)
\(\Leftrightarrow m=-3\)

Ta có : \(x^2-6=x\)
\(\Leftrightarrow x^2-6-x=0\)
\(\Leftrightarrow x^2+2x-3x-6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-2\\x=3\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{-2;3\right\}\)
\(x^2-7x+12=0\)
\(\Leftrightarrow x^2-3x-4x+12=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=4\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{3;4\right\}\)
Vậy nghiệm chung của 2 phương trình là x = 3
gfvfvfvfvfvfvfv555