Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phát biểuđúng: a , c, e, f, g, i, j, l
b. Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó có thể là phép tịnh tiến
d. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
h. Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có AB = A’B’.
k. Nếu phép dời hình biến điểm A thành điểm B thì nó cũng biến điểm B thành A (phát biểu không đúng với phép tịnh tiến)

a) Giả sử A'=(x'; y'). Khi đó \(T_{\overrightarrow{v}}\left(A\right)=A'\Leftrightarrow\left\{{}\begin{matrix}x'=3-1=2\\y'=5+2=7\end{matrix}\right.\)
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có: \(A=T_{\overrightarrow{v}}\left(C\right)\Leftrightarrow C=^T\overrightarrow{-v}\left(A\right)=\left(4;3\right)\)
c) Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = \(^T\overrightarrow{v}\) =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy \(^T\overrightarrow{v}\) (d) = d'.
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi \(^T\overrightarrow{v}\)(d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó \(^T\overrightarrow{v}\) (B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8.
a) Giả sử A'=(x'; y'). Khi đó
(A) = A' ⇔
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có A = (C) ⇔ C=
(A) = (4;3)
c)Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy
(d) = d'
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi (d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó
(B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8


- Dựng hình bình hành ABB'G và ACC'G. Khi đó ta có: \(\overrightarrow{AG}=\overrightarrow{BB'}=\overrightarrow{CC'}\)
. Suy ra \(^T\overrightarrow{AG}\left(A\right)=G,^T\overrightarrow{AG}\left(B\right)=B',^T\overrightarrow{AG}\left(C\right)=C'\)
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ \(\overrightarrow{AG}\) là tam giác GB'C'.
- Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có \(\overrightarrow{DA}=\overrightarrow{AG}\). Do đó, \(^T\overrightarrow{AG}\left(D\right)=A\).

- Dựng hình bình hành ABB'G và ACC'G. Khi đó ta có: −−→AG=−−→BB′=−−→CC′AG→=BB′→=CC′→
. Suy ra T−−→AG(A)=G,T−−→AG(B)=B′,T−−→AG(C)=C′TAG→(A)=G,TAG→(B)=B′,TAG→(C)=C′
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ −−→AGAG→ là tam giác GB'C'.
- Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có −−→DA=−−→AGDA→=AG→. Do đó, T−−→AG(D)=ATAG→(D)=A.

a)
Qua phép đối xứng trục Oy điểm \(M\left(1;1\right)\) biến thành điểm \(M'\left(x;y\right)\) có tọa độ là: \(\left\{{}\begin{matrix}x'=-x=-1\\y'=y=1\end{matrix}\right.\).
Suy ra: \(M'\left(-1;1\right)\).
Qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\left(2;0\right)\) điểm M' biến thành điểm \(A\left(x_A;y_A\right)\) là:\(\left\{{}\begin{matrix}x_A=-1+2=1\\y_A=0+1=1\end{matrix}\right.\).
Suy ra: \(A\left(1;1\right)\equiv M\) là điểm cần tìm.
b) Gọi C là ảnh của điểm M qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)
là: \(\left\{{}\begin{matrix}x_C=2+1=3\\y_C=0+1=1\end{matrix}\right.\). Suy ra: \(C\left(3;1\right)\)
\(M''=Đ_{Oy}\left(C\right)\) nên \(\left\{{}\begin{matrix}x_{M''}=-x_C=-3\\y_{M''}=y_C=1\end{matrix}\right.\). Suy ra: \(M''\left(-3;1\right)\).

M-> M' => VÊCTỚ MM'= VT u
Tv: M' -> M'' => vt M'M'' = v
áp dụng quy tắc 3 diểm => vt MM' +M'M'' = u+v =w
=> với mỗi điểm M qua phép tt theo vecto w se biến M -> M'' => ĐÓ LÀ PHÉP TT

a. Các phép biến một điểm A thành chính nó:
Phép đồng nhất:
- Phép tịnh tiến theo vectơ 0 .
- Phép quay tâm A, góc φ = 0º.
- Phép đối xứng tâm A.
- Phép vị tự tâm A, tỉ số k = 1.
- Ngoài ra còn có:
- Phép đối xứng trục mà trục đi qua A.
b. Các phép biến hình biến điểm A thành điểm B:
- Phép tịnh tiến theo vectơ AB .
- Phép đối xứng qua đường trung trực của đoạn thẳng AB.
- Phép đối xứng tâm qua trung điểm của AB.
- Phép quay mà tâm nằm trên đường trung trực của AB.
- Phép vị tự mà tâm là điểm chia trong hoặc chia ngoài đoạn thẳng AB theo tỉ số k.
c. Phép tịnh tiến theo vectơ v //d.
- Phép đối xứng trục là đường thẳng d’ ⊥ d.
- Phép đối xứng tâm là điểm A ∈ d.
- Phép quay tâm là điểm A ∈ d, góc quay φ =180º.
- Phép vị tự tâm là điểm I ∈ d.
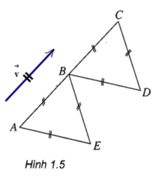


Phép tịnh tiến biến ba điểm A, B, E theo thứ tự thành ba điểm B, C, D là phép tịnh tiến theo v→ như hình vẽ trên: vecto v→=AB→