Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{8a^2+b}{4a}+b^2=2a+\frac{b}{4a}+b^2=a+a+\frac{b}{4a}+b^2\)
\(\ge a+1-b+\frac{1-a}{4a}+b^2=a+1-b+\frac{1}{4a}-\frac{1}{4}+b^2\)(do \(a+b\ge1\))
\(=\left(a+\frac{1}{4a}\right)+b^2-b+\frac{1}{4}+\frac{1}{2}\)
\(\ge2\sqrt{a\cdot\frac{1}{4a}}+\left(b-\frac{1}{2}\right)^2+\frac{1}{2}\)
\(\ge2\cdot\frac{1}{2}+\frac{1}{2}=\frac{3}{2}\)
Dấu = khi \(a=b=\frac{1}{2}\)


\(A=2a+\frac{b}{4a}+b^2=a+a+\frac{b}{4a}+b^2\)
\(A\ge a+1-b+\frac{1-a}{4a}+b^2\)
\(A\ge a+\frac{1}{4a}+b^2-b=a+\frac{1}{4a}+\left(b-\frac{1}{2}\right)^2-\frac{1}{4}\)
\(A\ge a+\frac{1}{4a}-\frac{1}{4}\ge2\sqrt{\frac{a}{4a}}-\frac{1}{4}=\frac{1}{4}\)
\(A_{min}=\frac{1}{4}\) khi \(\left\{{}\begin{matrix}a=\frac{1}{2}\\b=\frac{1}{2}\end{matrix}\right.\)
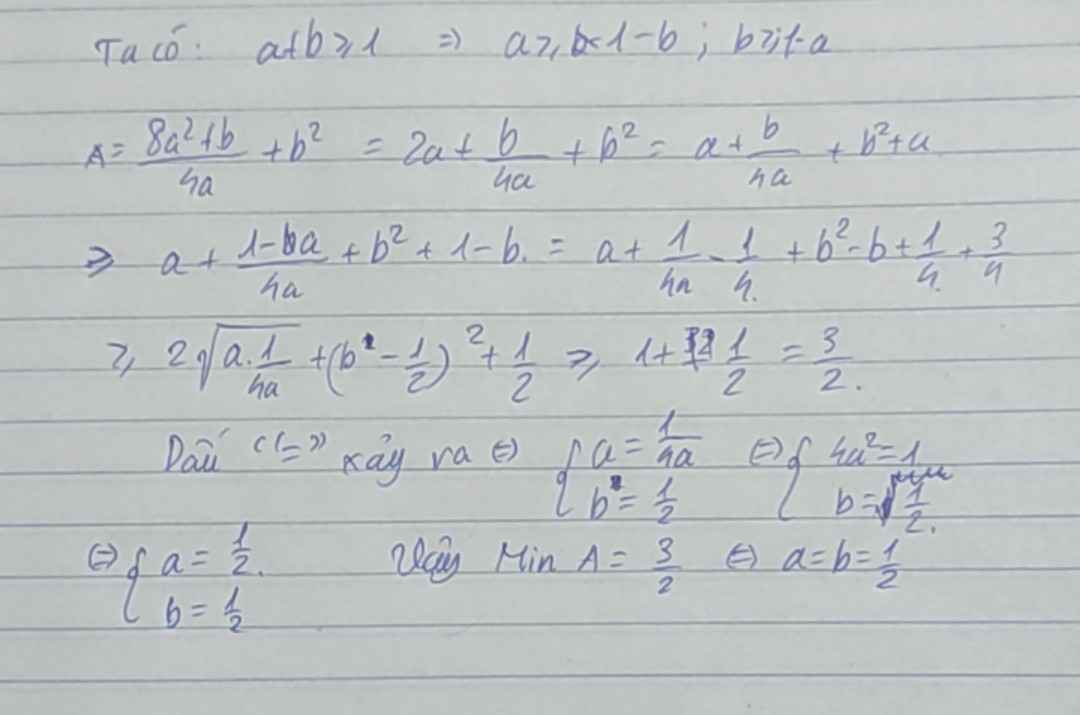

Do \(0< a< 1\Rightarrow b>0\)
\(A=2a+\frac{b}{4a}+b^2=\frac{3a}{2}+\frac{a}{2}+\frac{b}{4a}+b^2\ge\frac{3a}{2}+3\sqrt[3]{\frac{ab^3}{8a}}=\frac{3}{2}\left(a+b\right)\ge\frac{3}{2}\)
\(A_{min}=\frac{3}{2}\) khi \(a=b=\frac{1}{2}\)