
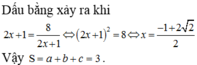
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

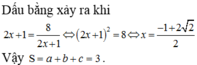

Bài 2: Mình nghĩ điều kiện sửa thành $a,b\in\mathbb{N}$ thôi thì đúng hơn.
ĐKĐB $\Leftrightarrow \log_2[(2x+1)(y+2)]^{y+2}=8-(2x-2)(y+2)$
$\Leftrightarrow (y+2)\log_2[(2x+1)(y+2)]=8-(2x-2)(y+2)$
$\Leftrightarrow (y+2)[\log_2[(2x+1)(y+2)]+(2x-2)]=8$
$\Leftrightarrow \log_2[(2x+1)(y+2)]+(2x-2)]=\frac{8}{y+2}$
$\Leftrightarrow \log_2(2x+1)+\log_2(y+2)+(2x+1)-3=\frac{8}{y+2}$
$\Leftrightarrow \log_2(2x+1)+(2x+1)=\frac{8}{y+2}+3-\log_2(y+2)=\frac{8}{y+2}+\log_2(\frac{8}{y+2})(*)$
Xét hàm $f(t)=\log_2t+t$ với $t>0$
$f'(t)=\frac{1}{t\ln 2}+1>0$ với mọi $t>0$
Do đó hàm số đồng biến trên TXĐ
$\Rightarrow (*)$ xảy ra khi mà $2x+1=\frac{8}{y+2}$
$\Leftrightarrow 8=(2x+1)(y+2)$
Áp dụng BĐT AM-GM:
$8=(2x+1)(y+2)\leq \left(\frac{2x+1+y+2}{2}\right)^2$
$\Rightarrow 2\sqrt{2}\leq \frac{2x+y+3}{2}$
$\Rightarrow 2x+y\geq 4\sqrt{2}-3$
Vậy $P_{\min}=4\sqrt{2}-3$
$\Rightarrow a=4; b=2; c=-3$
$\Rightarrow a+b+c=3$
Đáp án B.
2.
\(\Leftrightarrow\left(y+2\right)log_2\left(2x+1\right)\left(y+2\right)=8-\left(2x-2\right)\left(y+2\right)\)
\(\Leftrightarrow log_2\left(2x+1\right)\left(y+2\right)=\frac{8}{y+2}-2x+2\)
\(\Leftrightarrow log_2\left(2x+1\right)+log_2\left(y+2\right)=\frac{8}{y+2}-2x+2\)
\(\Leftrightarrow log_2\left(2x+1\right)+\left(2x+1\right)=-log_2\left(y+2\right)+3+\frac{8}{y+2}\)
\(\Leftrightarrow log_2\left(2x+1\right)+\left(2x+1\right)=log_2\left(\frac{8}{y+2}\right)+\frac{8}{y+2}\)
Xét hàm \(f\left(t\right)=log_2t+t\Rightarrow f'\left(t\right)=\frac{1}{t.ln2}+1>0;\forall t>0\)
\(\Rightarrow f\left(t\right)\) đồng biến \(\Rightarrow2x+1=\frac{8}{y+2}\)
\(\Rightarrow2x=\frac{8}{y+2}-1=\frac{6-y}{y+2}\)
\(\Rightarrow P=2x+y=y+\frac{6-y}{y+2}=y+\frac{8}{y+2}-1\)
\(\Rightarrow P=y+2+\frac{8}{y+2}-3\ge2\sqrt{\frac{8\left(y+2\right)}{y+2}}-3=4\sqrt{2}-3\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\\c=-3\end{matrix}\right.\) \(\Rightarrow a+b+c=3\)

\(\left\{{}\begin{matrix}x^2=2log_a\left(ab\right)=2\left(1+log_ab\right)\\y^2=2log_b\left(ab\right)=2\left(1+log_ba\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2log_ab=x^2-2\\2log_ba=y^2-2\end{matrix}\right.\) \(\Rightarrow\left(x^2-2\right)\left(y^2-2\right)=4\)
\(\Leftrightarrow y^2-2=\frac{4}{x^2-2}\Rightarrow y^2=\frac{2x^2}{x^2-2}\) (\(x\ge\sqrt{2}\))
\(\Rightarrow P=f\left(x\right)=8x+\frac{x\sqrt{2}}{\sqrt{x^2-2}}=0\)
\(\Rightarrow f'\left(x\right)=8-\frac{2\sqrt{2}x}{\left(x^2-2\right)^2\sqrt{\frac{x^2}{x^2-2}}}=0\)
\(\Leftrightarrow\left(x^2-2\right)^3=\frac{1}{8}\Leftrightarrow x^2-2=\frac{1}{2}\Rightarrow x=\frac{\sqrt{10}}{2}\)
\(\Rightarrow P_{min}=P\left(\frac{\sqrt{10}}{2}\right)=5\sqrt{10}\Rightarrow\left\{{}\begin{matrix}m=0\\n=5\\m=10\end{matrix}\right.\) \(\Rightarrow m+n+p=15\)

\(8,\dfrac{bc}{\sqrt{3a+bc}}=\dfrac{bc}{\sqrt{\left(a+b+c\right)a+bc}}=\dfrac{bc}{\sqrt{a^2+ab+ac+bc}}\)
\(=\dfrac{bc}{\sqrt{\left(a+b\right)\left(a+c\right)}}\le\dfrac{\dfrac{b}{a+b}+\dfrac{c}{a+c}}{2}\)
Tương tự cho các số còn lại rồi cộng vào sẽ được
\(S\le\dfrac{3}{2}\)
Dấu "=" khi a=b=c=1
Vậy
\(7,\sqrt{\dfrac{xy}{xy+z}}=\sqrt{\dfrac{xy}{xy+z\left(x+y+z\right)}}=\sqrt{\dfrac{xy}{xy+xz+yz+z^2}}\)
\(=\sqrt{\dfrac{xy}{\left(x+z\right)\left(y+z\right)}}\le\dfrac{\dfrac{x}{x+z}+\dfrac{y}{y+z}}{2}\)
Cmtt rồi cộng vào ta đc đpcm
Dấu "=" khi x = y = z = 1/3

3.
\(y'=-3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=0\end{matrix}\right.\)
\(y\left(-1\right)=m-2\) ; \(y\left(1\right)=m-4\)
\(\Rightarrow y_{min}=y\left(1\right)=m-4\)
\(\Rightarrow m-4=0\Rightarrow m=4\)
4.
Hàm đã cho bậc nhất trên bậc nhất nên đơn điệu trên mọi khoảng xác định
\(\Rightarrow y_{min}+y_{max}=y\left(1\right)+y\left(2\right)=\frac{m+1}{2}+\frac{m+2}{3}=8\)
\(\Rightarrow m=\frac{41}{5}\)
Đáp án B
1.
\(y'=\frac{1}{\left(sinx+1\right)^2}.cosx>0\Rightarrow y\) đồng biến
\(m=y_{min}=y\left(0\right)=2\)
\(M=y_{max}=y\left(1\right)=\frac{5}{2}\)
\(\Rightarrow M^2+m^2=\frac{41}{4}\)
2.
Hàm xác định trên \(\left[-2;2\right]\)
\(y'=1-\frac{x}{\sqrt{4-x^2}}=0\Leftrightarrow x=\sqrt{2}\)
\(y\left(-2\right)=-2\) ; \(y\left(\sqrt{2}\right)=2\sqrt{2}\) ; \(y\left(2\right)=2\)
\(\Rightarrow N=-2;M=2\sqrt{2}\)
\(\Rightarrow M+2N=2\sqrt{2}-4\)

1.
Hàm trùng phương có đúng 1 cực trị khi:
TH1: \(a=m=0\)
TH2: \(ab=-m>0\Leftrightarrow m< 0\)
\(\Rightarrow m\le0\)
Đáp án B
2.
\(y'=3\left(x^2+2mx+m^2-1\right)=3\left(x+m+1\right)\left(x+m-1\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=-m+1\\x=-m-1\end{matrix}\right.\)
Hàm số có 2 cực trị nằm về 2 phía trục hoành
\(\Leftrightarrow y'\left(-m+1\right).y'\left(-m-1\right)< 0\)
\(\Leftrightarrow\left(3m-2\right)\left(3m+2\right)< 0\Rightarrow-\frac{2}{3}< m< \frac{2}{3}\)
\(\Rightarrow a+2b=-\frac{2}{3}+2.\frac{2}{3}=\frac{2}{3}\)

Câu 2. Đặt A=x2+y2+1
Nhập \(2^A=\left(A-2x+1\right)4^x\) vào máy tính Casio. Cho x=0.01, tìm A
Máy sẽ giải ra, A=1.02=1+2x
\(\Leftrightarrow x^2+y^2+1=1+2x\)
\(\Leftrightarrow x^2+y^2-2x=1\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=1\) (C)
Có (C) là đường tròn tâm (1,0) bán kính R=1
Lại có: P=\(\frac{8x+4}{2x-y+1}\)
\(\Leftrightarrow x\left(2P-8\right)-yP+P-4=0\) (Q)
Có (Q) là phương trình đường thẳng.
Để x,y có nghiệm thì đường thẳng và đường tròn giao nhau nghĩa là d(I,(Q))\(\le R\)
\(\Leftrightarrow\frac{\left|x\left(2P-8\right)-yP+P-4\right|}{\sqrt{\left(2P-8\right)^2+P^2}}\le1\)
\(\Leftrightarrow\frac{\left|2P-8+P-4\right|}{\sqrt{\left(2P-8\right)^2+1}}\le1\)
\(\Leftrightarrow\left(3P-12\right)^2\le5P^2-32P+64\)
\(\Leftrightarrow4P^2-40P+80\le0\)
\(\Leftrightarrow5-\sqrt{5}\le P\le5+\sqrt{5}\)
Vậy GTNN của P gần số 3 nhất. Chọn C