K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 5 2018
Không mất tính tổng quát,
Giả sử a<b
Ta có: ab=bc => c<b
Ta có: bc=cd => c<d
Ta có: cd=de => e<d
Ta có: de=ea => a>e
Ta có: ea=ab => a>b ( trái với giả sử)
Vậy a=b=c=d=e
=> ba=bc=cd=de=ea
e<a
31 tháng 12 2018
câu 4:
a) ĐK: x≠ 0
b) \(A=x^2-x+1\)
sa thì sửa
Cúc bạn học tốt
15 tháng 12 2022
Bài 5:
a: H đối xứng với D qua AB
nên HD vuông góc với AB tại trung điểm của HD
=>AB là phân giác của góc HAD(1)
H đối xứng với E qua AC
nên HE vuông góc với AC tại trung điểm của HE
=>AC là phân giác của góc HAE(2)
Xét tứ giác AIHK có
góc AIH=góc AKH=góc KAI=90 độ
nên AIHK là hình chữ nhật
b: Từ (1), (2) suy ra góc EAD=2*90=180 độ
=>E,A,D thẳng hàng
Với hai phân thức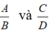
,ta tìm được hai phân thức cùng mẫu 
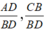, và thỏa mãn điều kiện :
Ta nhân tử và mẫu của hai phân thức đó với cùng một đa thức M ≠ 0 bất kỳ, ta có hai phân thức mới cùng mẫu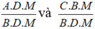
và lần lượt bằng hai phân thức 
.
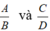Đặt B.D.M = E, A.D.M = A', C.B.M = C' ta có:
Vì có vô số đa thức M ≠ 0 nên ta có vô số phân thức cùng mẫu bằng hai phân thức đã cho.