Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ Khi \(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow\cos\left(\widehat{F_1;F_2}\right)=\cos0=0\)
\(\Rightarrow F^2=F_1^2+F_2^2\Leftrightarrow F=\sqrt{6^2+6^2}=6\sqrt{2}\left(N\right)\)
2/ \(F^2=F_1^2+F_2^2+2.F_1.F_2.\cos\left(\widehat{F_1;F_2}\right)\)
\(F=\sqrt{6^2+6^2+2.6.6.\cos120}=6\left(N\right)\)

Chọn đáp án C
Hai lực thành phần F1 = F2 hợp nhau bất kỳ thì hợp lực:
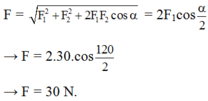

a.Ta có lực tổng hợp thỏa mãn tính chất
F min ≤ F ≤ F max ⇒ F 1 − F 2 ≤ F ≤ F 1 + F 2 ⇒ 1 N ≤ F ≤ 7 N
Vậy hợp lực của chúng có thể là 5N
b. Ta có
F 2 = F 1 2 + F 2 2 + 2 F 1 F 2 cos α ⇒ 5 2 = 3 2 + 4 2 + 2.3.4. cos α ⇒ α = 90 0

Đáp án D
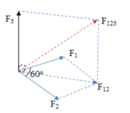
Hợp lực của F1 và F2 là:
F 12 = 2. F 1 . cos α 2 = 2.20. cos 30 0 = 20 3 N
F3 vuông góc với mp chứa F1 và F2 nên F3 vuông góc với F12.
Hợp lực của ba lực chính là hợp lực của F12 và F3.
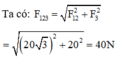
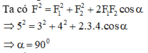
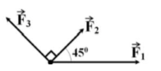

Áp dụng công thức: \(F^2=F_1^2+F_2^2+2.F_1.F_2.\cos\left(\widehat{F_1;F_2}\right)\)
a/ \(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow\left(\widehat{F_1;F_2}\right)=0\Rightarrow\cos0=0\)
Thay số vào tìm đc F
b/ \(\overrightarrow{F_1}\uparrow\downarrow\overrightarrow{F_2}\Rightarrow\left(\widehat{F_1;F_2}\right)=180^0\Rightarrow\cos\left(\widehat{F_1;F_2}\right)=-1\)
Thay vào
c/ \(\left(\widehat{F_1;F_2}\right)=90^0\Rightarrow\cos90^0=0\)
d/ làm tương tự
Là nn ạ, mk ko hiểu