Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để đồ thị hàm số tạo với 2 trục 1 tam giác \(\Rightarrow m\ne\left\{1;2\right\}\)
Gọi A và B lần lượt là giao điểm của ĐTHS với Ox và Oy
\(\Rightarrow A\left(-\dfrac{m-2}{m-1};0\right)\) ; \(B\left(0;m-2\right)\)
\(\Rightarrow OA=\left|-\dfrac{m-2}{m-1}\right|=\left|\dfrac{m-2}{m-1}\right|\) ; \(OB=\left|m-2\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=2\Rightarrow OA.OB=4\)
\(\Leftrightarrow\left|\dfrac{m-2}{m-1}\right|.\left|m-2\right|=4\Leftrightarrow\left(m-2\right)^2=4\left|m-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2-4m+4=4\left(m-1\right)\\m^2-4m+4=-4\left(m-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2-8m+8=0\\m^2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=4\pm2\sqrt{2}\\m=0\end{matrix}\right.\)

A học đại học rồi mà vẫn hỏi câu lp 9 ak

a, Thay x = -2 => y = -2 + 4 = 2 => A(-2;2)
(d) cắt y = x + 4 tại A(-2;2) <=> 2 = -2 ( m + 1 ) - 2
<=> -2m - 2 - 2 = 2 <=> -2m = 6 <=> m = -3
Vậy (d) : y = -2x - 2
b, bạn tự vẽ nhé
c, Cho x = 0 => y = -2
=> (d) cắt trục Oy tại A(0;-2) => OA = | -2 | = 2
Cho y = 0 => x = -1
=> (d) cắt trục Ox tại B(-1;0) => OB = | -1 | = 1
Ta có : \(S_{OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}.2.1=1\)( dvdt )
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\hept{m+5=22m−10≠−1\hept{m+5=22m−10≠−1 <=> \hept{m=−3m≠92\hept{m=−3m≠92 <=> m=−3
Giả sử (d) luôn đi qua điểm cố định M(x0; y0)
Ta có: y0=(m+5)x0+2m−10y0=(m+5)x0+2m−10
<=> mx0+5x0+2m−10−y0=0mx0+5x0+2m−10−y0=0
<=> m(xo+2)+5x0−y0−10=0m(xo+2)+5x0−y0−10=0
Để M cố định thì: \hept{x0+2=05x0−y0−10=0\hept{x0+2=05x0−y0−10=0 <=> \hept{x0=−2y0=−20\hept{x0=−2y0=−20
Vậy...

cho x=0=>y=m+3=>A(0;m+3)
cho y=0=>\(x=\dfrac{-m-3}{m-2}\)\(=>B\left(\dfrac{-m-3}{m-2};0\right)\)
vậy đồ thị hàm số trên là đường thẳng đi qua A(0,m+3) và B\(\left(\dfrac{-m-3}{m-2};0\right)\)
\(=>S\left(\Delta OAB\right)=1=\dfrac{OA.OB}{2}=\dfrac{\left(m+3\right)\left(\dfrac{-m-3}{m-2}\right)}{2}\)
\(=>m=..............\)(bạn tự tính)

c) y = (m – 3)x + 2 (m ≠ 3)
Gọi A, B lần lượt là giao điểm của (d) và trục Ox, Oy và tam giác tạo thành là tam giác AOB vuông tại O
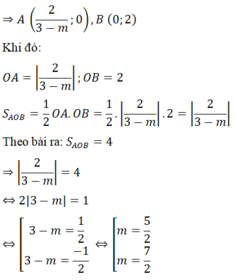

Để hàm số y=(m-2)x+4+m là hàm số bậc nhất thì \(m-2\ne0\)
hay \(m\ne2\)
a) Để đồ thị hàm số y=(m-2)x+4+m đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số y=(m-2)x+4+m, ta được
\(\left(m-2\right)\cdot1+4+m=2\)
\(\Leftrightarrow m-1+4+m=2\)
\(\Leftrightarrow2m+3=2\)
\(\Leftrightarrow2m=-1\)
hay \(m=-\dfrac{1}{2}\)(nhận)
Vậy: Để đồ thị hàm số y=(m-2)x+4+m đi qua điểm A(1;2) thì \(m=-\dfrac{1}{2}\)

Nếu m = 4 => y = -5
Đường thẳng y = -5 song song với trục Ox , khi đó sẽ ko có tam giác
=> m = 4 (loại)
Do đó m \(\ne\)4
O y x A B
*Tại x = 0 thì y = -5
=> Giao điểm của đths y = ( 4 - m )x - 5 với trục Oy là điểm A(0;-5)
\(\Rightarrow OA=\sqrt{\left(0-0\right)^2+\left[0-\left(-5\right)\right]^2}=5\)
*Tại y = 0 thì \(x=\frac{5}{4-m}\)
=> giao điểm của đths y = (4 - m)x - 5 với trục Ox là điểm \(B\left(\frac{5}{4-m};0\right)\)
\(\Rightarrow OB=\sqrt{\left(0-\frac{5}{4-m}\right)^2+\left(0-0\right)^2}=\frac{5}{\left|4-m\right|}\)
Vì \(S_{AOB}=3\)mà tam giác này vuông tại O
\(\Rightarrow OA.OB=3\)
\(\Leftrightarrow5.\frac{5}{\left|4-m\right|}=3\)
\(\Leftrightarrow\frac{25}{\left|4-m\right|}=3\)
\(\Leftrightarrow\left|4-m\right|=\frac{25}{3}\)
\(\Leftrightarrow\orbr{\begin{cases}4-m=\frac{25}{3}\\4-m=-\frac{25}{3}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m=-\frac{13}{3}\\m=\frac{37}{3}\end{cases}}\left(TmĐK:m\ne4\right)\)
Vậy \(m\in\left\{-\frac{13}{3};\frac{37}{3}\right\}\)thỏa mãn bài toán
m=-1/2
PT giao Ox: \(y=0\Leftrightarrow x=\dfrac{-\left(2m+4\right)}{m+2}=-2\Leftrightarrow A\left(-2;0\right)\Leftrightarrow OA=2\)
PT giao Oy: \(x=0\Leftrightarrow y=2m+4\Leftrightarrow B\left(0;2m+4\right)\Leftrightarrow OB=2\left|m+2\right|\)
\(S_{OAB}=3\Leftrightarrow\dfrac{1}{2}OA\cdot OB=3\Leftrightarrow OB=3\\ \Leftrightarrow2\left|m+2\right|=3\Leftrightarrow\left|m+2\right|=\dfrac{3}{2}\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}-2=-\dfrac{1}{2}\\m=-\dfrac{3}{2}-2=-\dfrac{7}{2}\end{matrix}\right.\)