
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

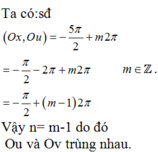

Số đo của các góc lượng giác tia đầu $O u$, tia cuối $O v$ là
\(sđ(O u, O v) = sđ(O x, O v) - sđ(O x, O u)+ k{360}^{\circ}(k \in \mathbb{Z}) \)
\(=-270^{\circ}-240^{\circ}+k 360^{\circ}=-510^{\circ}+k 360^{\circ} \)
\( =-150^{\circ}+(k-1) 360^{\circ}=-150^{\circ}+n 360^{\circ} \quad(n=k-1, n \in \mathbb{Z})
\)
Vậy các góc lượng giác $(O u, O v)$ có số đo là $-150^{\circ}+n 360^{\circ} \quad(n \in \mathbb{Z})$.

Vì sao là 3 mà không phải là 4. Có phép quay tâm ở góc 0, 60, 120, 360

a/ \(y'=2cos2x=0\Rightarrow cos2x=0\Rightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
Do \(x\in\left[0;\frac{\pi}{2}\right]\Rightarrow x=\frac{\pi}{4}\)
\(cos2x< 0\) khi \(\frac{\pi}{4}< x< \frac{\pi}{2}\); \(cos2x>0\) khi \(0< x< \frac{\pi}{4}\)
Hàm số đồng biến trên \(\left(0;\frac{\pi}{4}\right)\) nghịch biến trên \(\left(\frac{\pi}{4};\frac{\pi}{2}\right)\)
b/ \(y'=-2sin2x=0\Rightarrow sin2x=0\Rightarrow x=\frac{k\pi}{2}\)
Do \(x\in\left(-\frac{\pi}{4};\frac{\pi}{4}\right)\Rightarrow x=0\)
Hàm số đồng biến trên \(\left(-\frac{\pi}{4};0\right)\) nghịch biến trên \(\left(0;\frac{\pi}{4}\right)\)

\(cos\left(\frac{x}{2}+15^0\right)=sinx=cos\left(90^0-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}\frac{x}{2}+15^0=90^0-x+k360^0\\\frac{x}{2}+15^0=x-90^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=50^0+k240^0\\x=210^0+k720^0\end{matrix}\right.\)
Với \(k=1\Rightarrow x=290^0\)
Bài 2:
\(\Leftrightarrow2sinx+2sinx.cosx-cosx-cos^2x-sin^2x=0\)
\(\Leftrightarrow2sinx+2sinx.cosx-cosx-1=0\)
\(\Leftrightarrow2sinx\left(cosx+1\right)-\left(cosx+1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(cosx+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\cosx=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\) đáp án B
3/ \(y=\frac{sinx+cosx-1}{sinx-cosx+3}\)
\(\Leftrightarrow y.sinx-y.cosx+3y=sinx+cosx-1\)
\(\Leftrightarrow\left(y-1\right)sinx-\left(y+1\right)cosx=-3y-1\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(y-1\right)^2+\left(y+1\right)^2\ge\left(-3y-1\right)^2\)
\(\Leftrightarrow7y^2+6y-1\le0\)
\(\Rightarrow-1\le y\le\frac{1}{7}\Rightarrow y_{max}=\frac{1}{7}\)