Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)ME.MO = MA2 (hệ thức lượng trong MAO vuông)
MF.MO’ = MA2 (hệ thức lượng trong MAO’ vuông)
Suy ra ME.MO = MF.MO’
c)Đường tròn có đường kính BC có tâm M, bán kính MA.OO’ vuông góc với MA tại A nên là tiếp tuyến của đường tròn (M).
d)Hình b
Gọi I là trung điểm của OO’, I là tâm của đường tròn có đường kính OO’, IM là bán kính (vì MI là trung tuyến ứng với cạnh huyền của MOO’. IM là đường trung bình của hình thang OBCO’ nên IM // OB // O’C. Do đó IM ⊥ BC.
BC vuông góc với IM tại M nên BC là tiếp tuyến của đường tròn (I).

Đường tròn có đường kính BC có tâm M, bán kính MA.OO' vuông góc với MA tại A nên là tiếp tuyến của đường tròn (M).

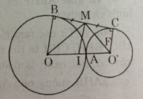
Gọi I là trung điểm của OO', I là tâm của đường tròn có đường kính OO', IM là bán kính (vì MI là trung tuyến ứng với cạnh huyền của MOO'. IM là đường trung bình của hình thang OBCO' nên IM // OB // O'C. Do đó IM ⊥ BC.
BC vuông góc với IM tại M nên BC là tiếp tuyến của đường tròn (I).

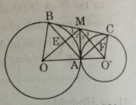
MA và MB là các tiếp tuyến của (O) (gt).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
MA = MB
MO là tia phân giác của góc AMB
ΔAMB cân tại M (MA = MB) mà có MO là đường phân giác nên đồng thời là đường cao
=> MO ⊥ AB hay ∠MEA = 90o
Tương tự ta có MO' là tia phân giác của góc AMC và ∠MFA = 90o
MO, MO' là tia phân giác của hai góc kề bù ∠AMB và ∠AMC nên ∠EMF = 90o
=> Tứ giác AEMF là hình chữ nhật (vì có ba góc vuông).

ME.MO = MA2 (hệ thức lượng trong ΔMAO vuông)
MF.MO' = MA2 (hệ thức lượng trong ΔMAO' vuông)
Suy ra ME.MO = MF.MO'

Mừng quá. Xong hết rồi. Hơn nửa tiếng bây giờ cũng được đền đáp =))
a) MB = MC (=MA) (giao điểm 2 tiếp tuyến cách đều tiếp điểm)
b) MA = MB = MC => T/g ABC vuông tại A => ^A = 90
T/g OAB cân tại O, có OM là đ/phân giác nên OM cũng là đ cao hay ^ANM = 90
Tương tự, ^APM = 90
=> đpcm
c) MO'/MO = O'C/BM (CMO' ~ BOM) = O'C/CM = CP/MP (CMO' ~ PMC) = MN/MP (PMC = NBM góc vuông - cạnh huyền - góc nhọn so le trong)
=> đpcm
d) Trong t/g vuông OMO' có MA là đường cao, OM^2 = OA.OO' <=> OM = 20 => BM = 12 (Pytago) => BC = 24
e) Dùng ta lét tìm ra OE, EC, còn OC tìm theo pytago trong t/g vuông OBC
f) ABKC là hình chữ nhật => AK cắt BC tại trung điểm M => đpcm

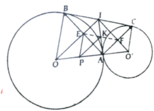
a, Chứng minh tứ giác AEIF là hình chữ nhật và K là trung điểm AI
b, Có IE.IO = I B 2 = B C 2 4 và IF.IO' = I C 2 = B C 2 4
=> 2.(IE.IO+IF.IO') = A B 2 + A C 2
c, PK Là đường trung bình của ∆OAI và là trung trực của EA
Ta có ∆PEK = ∆PAK nên P E K ^ = P A K ^
Vậy P E K ^ = 90 0 => đpcm
d, ∆ABC:∆IOO’ => S A B C S I O O ' = B C O O ' 2 => S A B C = S I O O ' . B C 2 O O ' 2
mà BC = 2AI'; OO' = 2a; S O I O ' = 1 2 . 2 a . I A = a . I A => S A B C = I A 2 a
I A 2 = R R ' ⩽ R + R ' 2 2 = a 2 => IA lớn nhất bằng a khi R=R’

Câu này khó đấy = )) Làm sai chỗ nào tự sửa
B M C E F O A O'
a) MA và MB là các tiếp tuyến của (O) ( gt )
Theo tính chất của hai tiếp tuyến cắt nhau , ta có :
MA = MB
MO là tia phân giác của góc AMB
Tam giác AMB cân tại M ( MA = MB ) mà có MO là đường phân giác nên đồng thời là đường cao
=> \(MO\perp AB\) hay góc MEA = 90o
Tương tự ta có MO' là tia phân giác của góc AMC và góc MFA = 90o
MO, MO' là tia phân giác của hai góc kề bù góc AMB và góc AMC nên góc EMF = 90o
=> Tứ giác AEMF là hình chữ nhật ( vì có ba góc vuông )
b) ME . MO = MA2 ( hệ thức lượng trong tam giác MAO vuông )
MF . MO' = MA2 ( hệ thức lượng trong tam giác MAO' vuông )
=> ME . MO = MF . MO'
c) Đường tròn có đường kính BC có tâm M, bán kính MA . OO' vuông góc với MA tại A nên là tiếp tuyến của đường tròn (M)
d)
Gọi I là trung điểm của OO'
- I là tâm của đường tròn có đường kính OO'
- IM là bán kính ( vì MI là trung tuyến ứng với cạnh huyền của MOO' )
- IM là đường trung bình của hình thang OBCO' nên IM // OB // O'C
=> Do đó \(IM\perp BC\)
BC vuông góc với IM tại M nên BC là tiếp tuyến của đường tròn (I)

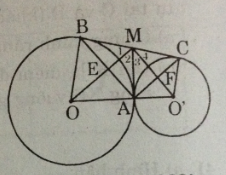
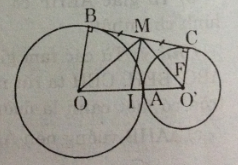
a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB và MO là phân giác của góc AMB
Xét (O') có
MA,MC là các tiếp tuyến
Do đó: MA=MC và MO' là phân giác của góc AMC
MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}\)
MO' là phân giác của góc AMC
=>\(\widehat{AMC}=2\cdot\widehat{AMO'}\)
Ta có: \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{AMO}+\widehat{AMO'}\right)=180^0\)
=>\(2\cdot\widehat{OMO'}=180^0\)
=>\(\widehat{OMO'}=90^0\)
=>MO\(\perp\)MO'
b: Ta có: MA=MC
=>M nằm trên đường trung trực của AC(1)
Ta có: OA=OC
=>O' nằm trên đường trung trực của AC(2)
Từ (1),(2) suy ra MO' là đường trung trực của AC
=>MO'\(\perp\)AC tại F
Ta có: MA=MB
=>M nằm trên đường trung trực của AB(3)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(4)
Từ (3),(4) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại E
Xét ΔMAO vuông tại A có AE là đường cao
nên \(ME\cdot MO=MA^2\left(5\right)\)
Xét ΔMAO' vuông tại A có AF là đường cao
nên \(MF\cdot MO'=MA^2\left(6\right)\)
Từ (5),(6) suy ra \(ME\cdot MO=MF\cdot MO'\)
=>\(\dfrac{ME}{MO'}=\dfrac{MF}{MO}\)
Xét ΔMEF và ΔMO'O có
\(\dfrac{ME}{MO'}=\dfrac{MF}{MO};\widehat{EMF}\) chung
Do đó: ΔMEF~ΔMO'O
=>\(\widehat{MFE}=\widehat{EOO'}\)