Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(f\left(x\right)=0\), do đó với mọi giá trị của x thì đa thức này bằng 0
Ta có:
\(f\left(1\right)=a.1^2+b.1+c=a+b+c=0\)
\(\Rightarrow a+b+c+3=0+3=3\)
Vậy \(a+b+c=3\)

Từ dãy tỉ số bằng nhau đó, ta được:
\(\frac{2a+b+c+d}{a}-1=\frac{a+2b+c+d}{b}-1=\frac{a+b+2c+d}{c}-1=\frac{a+b+c+2d}{d}-1\)
hay \(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}=\frac{4\left(a+b+c+d\right)}{a+b+c+d}=4\)
Do đó, \(\frac{a+b+c+d}{a}=4\) => a=\(\frac{a+b+c+d}{4}\)
\(\frac{a+b+c+d}{b}=4\) =>b=\(\frac{a+b+c+d}{4}\)
\(\frac{a+b+c+d}{c}=4\) =>c=\(\frac{a+b+c+d}{4}\)
\(\frac{a+b+c+d}{d}=4\) => d=\(\frac{a+b+c+d}{4}\)
=>a=b=c=d
a+bc+d
Do đó, M=\(\frac{a+b}{c+d}+\frac{b+c}{c+d}+\frac{c+d}{a+b}+\frac{d+a}{b+c}=\frac{a+a}{a+a}+\frac{a+a}{a+a}+\frac{a+a}{a+a}+\frac{a+a}{a+a}=1+1+1+1=4\)
Vậy M có giá trị là 4

Thay K(0) = 4 vào đa thức K(x) ta có : a.0^2 + b.0 + c => c = 4 (1)
Thay K(1) = 3 và (1) vào đa thức K(x) ta có : a.1^2 + b.1 + 4 = a + b + 4 = 3 => a+b=-1 => a= -1 - b (2)
Thay K(-1) = 7 , (1) vào đa thức K(x) ta có : a.(-1)^2 + b.(-1) + 4 = a-b+4=7 => a-b=3 (3)
Thay (2) vào (3) ta có : -1 - b - b = -1 - 2b = 3 => 2b= -4 => b = -2
Thay b = -2 vào (3) ta có : a - (-2) = 3 => a = 1.
Vậy a + b + c = 1 + (-2) + 4 = 3

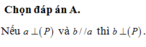
Đáp án A