Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo:
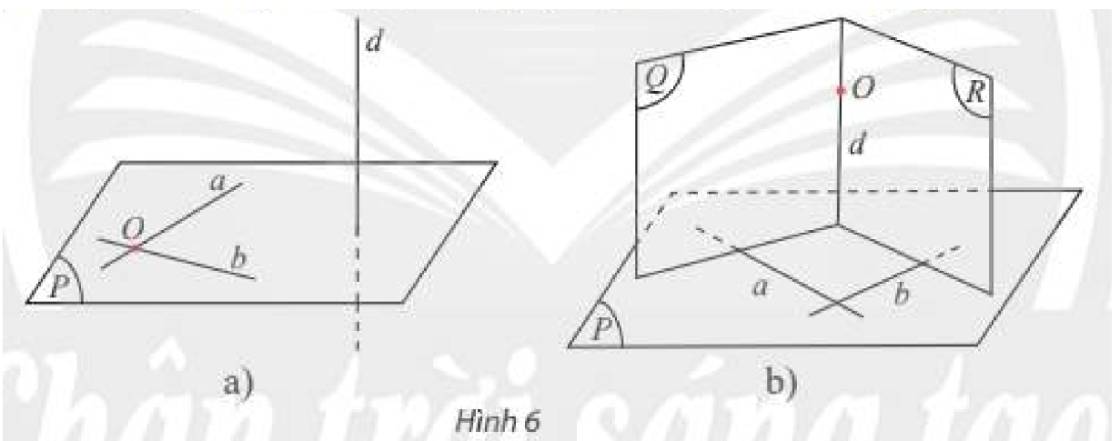
a) Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)
b) Vì a⊥(Q);d∈(Q) nên a⊥d
Vì b⊥(R),d∈(R) nên b⊥d
Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)

Đáp án C
Có 4 vị trí: song song, chéo nhau, cắt nhau. ( chú ý 2 đường thẳng a và b là 2 đường thẳng phân biệt nên không thể trùng nhau)

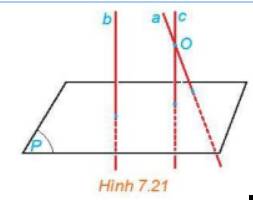
a) b // c; b ⊥ (P) ⇒ c ⊥ (P)
Mà a ⊥ (P)
a, c cùng đi qua điểm O
⇒ a trùng c.
b) Ta có b // c mà a trùng c nên a // b.

a: \(\text{Δ}\perp a\)
a//a'
=>Δ vuông góc a'
mà Δ vuông góc (P)
nên a'//(P) hoặc \(a'\subset\left(P\right)\)
mà \(a'\cap\left(P\right)=\left\{O\right\}\)
nên a' nằm trong (P)
b: a'//a
\(a'\subset\left(P\right)\)
=>a//(P) hoặc \(a\subset\left(P\right)\)

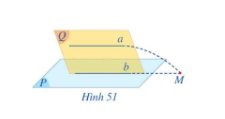
a) Ta có a ∩ b = {M} nên M ∈ b
Mà b ⊂ (P), do đó M ∈ (P).
Lại có M ∈ a.
Vậy đường thẳng a cắt mặt phẳng (P) tại M.
b) Theo câu a, nếu a cắt b tại M thì a cắt (P) tại M, điều này mâu thuẫn với giả thiết đường thẳng a song song với mặt phẳng (P).
Do đó a và b không cắt nhau và cùng nằm trong mặt phẳng (Q).
Suy ra a // b.
Vậy hai đường thẳng a và b song song với nhau.
Chọn D