Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức cos =
ta có cos =
=> cos =
=
=
=>
= 450

Bài 2:
Đường tròn \(\left(C_1\right)\) tâm \(\left(1;2\right)\) bán kính \(R=2\)
a/ Không hiểu đề bài, bạn ghi rõ thêm ra được chứ?
Tiếp tuyến đi qua giao điểm của \(\Delta_1;\Delta_2\) hay tiếp tuyến tại các giao điểm của \(\Delta_1\) và \(\Delta_2\) với đường tròn?
b/ Lại không hiểu đề nữa, điểm I trong tam giác \(IAB\) đó là điểm nào vậy bạn?
Bài 1b/
\(\Delta'\) nhận \(\left(2;1\right)\) là 1 vtpt
Gọi vtpt của d' có dạng \(\left(a;b\right)\Rightarrow\frac{\left|2a+b\right|}{\sqrt{2^2+1^2}.\sqrt{a^2+b^2}}=\frac{1}{\sqrt{2}}\)
\(\Leftrightarrow\sqrt{2}\left|2a+b\right|=\sqrt{5\left(a^2+b^2\right)}\Leftrightarrow2\left(2a+b\right)^2=5\left(a^2+b^2\right)\)
\(\Leftrightarrow3a^2+8ab-3b^2=0\Rightarrow\left[{}\begin{matrix}a=-3b\\3a=b\end{matrix}\right.\)
\(\Rightarrow\) d' có 2 vtpt thỏa mãn là \(\left(3;-1\right)\) và \(\left(1;3\right)\)
TH1: d' có pt dạng \(3x-y+c=0\)
\(d\left(I;d'\right)=R\Leftrightarrow\frac{\left|3.1-3+c\right|}{\sqrt{3^2+1^2}}=2\Rightarrow c=\pm2\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}3x-y+2\sqrt{10}=0\\3x-y-2\sqrt{10}=0\end{matrix}\right.\)
TH2: d' có dạng \(x+3y+c=0\)
\(d\left(I;d'\right)=R\Leftrightarrow\frac{\left|1+3.3+c\right|}{\sqrt{10}}=2\Leftrightarrow\left|c+10\right|=2\sqrt{10}\Rightarrow c=-10\pm2\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}x+3y-10+2\sqrt{10}=0\\x+3y-10-2\sqrt{10}=0\end{matrix}\right.\)

Bài 3:
Gọi M là giao điểm \(d_1;d_2\Rightarrow\) tọa độ M là nghiệm:
\(\left\{{}\begin{matrix}x+y-1=0\\x-3y+3=0\end{matrix}\right.\) \(\Rightarrow M\left(0;1\right)\)
Gọi \(A\left(1;0\right)\) là 1 điểm thuộc \(d_1\)
\(d_3\) đối xứng \(d_2\) qua \(d_1\Leftrightarrow d_1\) là phân giác góc tạo bởi \(d_2;d_3\)
\(\Rightarrow d_3\) qua M và \(d\left(A;d_3\right)=d\left(A;d_2\right)\)
Gọi pt \(d_3\) có dạng \(a\left(x-0\right)+b\left(y-1\right)=0\Leftrightarrow ax+by-b=0\)
Theo công thức khoảng cách:
\(\frac{\left|a.1+b.0-b\right|}{\sqrt{a^2+b^2}}=\frac{\left|1-3.0+3\right|}{\sqrt{1+3^2}}\Leftrightarrow\frac{\left|a-b\right|}{\sqrt{a^2+b^2}}=\frac{\sqrt{8}}{\sqrt{5}}\)
\(\Leftrightarrow5\left(a-b\right)^2=8\left(a^2+b^2\right)=3a^2+10ab+3b^2=0\)
\(\Leftrightarrow\left(a+3b\right)\left(3a+b\right)=0\Rightarrow\left[{}\begin{matrix}a=-3b\\b=-3a\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}-3bx+by-b=0\\ax-3ay+3a=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}3x-y+1=0\\x-3y+3=0\end{matrix}\right.\)
Bài 2:
a/ Gọi d' là đường thẳng qua M và vuông góc d
\(\Rightarrow d'\) nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình d':
\(2\left(x-2\right)-1\left(y-5\right)=0\Leftrightarrow2x-y+1=0\)
H là giao điểm của d và d' nên tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x+2y-2=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow H\left(0;1\right)\)
b/ M' đối xứng M qua d \(\Leftrightarrow H\) là trung điểm \(MM'\)
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M\\y_{M'}=2y_H-y_M\end{matrix}\right.\) \(\Rightarrow M'\left(-2;-3\right)\)
c/ d' đối xứng d qua M \(\Rightarrow\) phương trình d' có dạng: \(x+2y+c=0\) với \(c\ne-2\)
Ta có: \(d\left(M;d\right)=d\left(M;d'\right)\)
\(\Leftrightarrow\frac{\left|2+2.5-2\right|}{\sqrt{1^2+2^2}}=\frac{\left|2+2.5+c\right|}{\sqrt{1^2+2^2}}\)
\(\Rightarrow\left|c+12\right|=10\Rightarrow\left[{}\begin{matrix}c=-2\left(l\right)\\c=-22\end{matrix}\right.\)
Phương trình d': \(x+2y-22=0\)

Bài 2:
Tọa độ giao điểm của Δ1 và Δ2 là:
\(\left\{{}\begin{matrix}2x+y=4\\5x-2y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{9}\\y=\dfrac{26}{9}\end{matrix}\right.\)
Thay x=5/9 và y=26/9 vào Δ3, ta được:
\(\dfrac{5}{9}m+\dfrac{26}{3}-2=0\)
=>5/9m=-20/3
hay m=-12

Bạn tham khảo:
Câu hỏi của Lê Ngọc Cương - Toán lớp 9 | Học trực tuyến
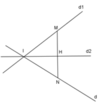
Đáp án D
Gọi I là giao điểm của hai đường thẳng d1; d2 . Tọa độ điểm I là nghiệm của hệ:
Lấy điểm m 1 ; 0 ∈ d 1 . Đường thẳng qua M và vuông góc với d2 có phương trình: 3x + y-3= 0
Gọi H = ∆ ∩ d 2 suy ra tọa độ điểm H là nghiệm của hệ:
Phương trình đường thẳng
có dạng:
hay x-3y + 3= 0