Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
a và b chéo nhau. Có duy nhất một mặt phẳng chứa a và song song với b vì có duy nhất một mặt phẳng chứa hai đường thẳng cắt nhau.

a) (P) có vec tơ pháp tuyến là \(\overrightarrow{n_1}\left(1;1;1\right)\)
\(\overrightarrow{AB}\left(1;-1;-1\right)\)
Vì (Q) vuông góc với mp (P) và chứa A; B nên véc tơ pháp tuyến của (Q) là \(\overrightarrow{n_2}\) vuông góc với cả \(\overrightarrow{n_1}\left(1;1;1\right)\) và \(\overrightarrow{AB}\left(1;-1;-1\right)\)
=> \(\overrightarrow{n_2}\) = \(\left[\overrightarrow{n_1};\overrightarrow{AB}\right]\) = (0; 2; -2)
mp(Q) đi qua A (-1;2;2) và có vec tơ pt là \(\overrightarrow{n_2}\) có phương trình là: 0.(x +1) + 2(y - 2) -2.(z - 2) = 0 <=> 2y - 2z = 0 <=> y - z = 0
b) đường thẳng AB có vec tơ chỉ phương là \(\overrightarrow{AB}\left(1;-1;-1\right)\) và đi qua B(0;1;1) có phương trình tham số là:
\(\begin{cases}x=t\\y=1-t\\z=1-t\end{cases}\left(t\in R\right)\)
H = AB giao với (P)
H thuộc AB => H (a; 1-a; 1 - a)
H thuộc mp(P) => a + 1- a+ 1 - a = 0 => 2 - a = 0 => a = 2
Vậy H (2; -1; -1)

bài 1
\(A+B=a+b-5-b-c+1=a-c-4\)
\(A+B+C+D=a-c-4+b-c-4+b-a=2b-2c\)
\(A-B+C-D=a+b-5+b+c-1+b-c-4+a-b\)
\(A-B+C-D=2a+2b-10\)
\(A+B=a-c-4\)
\(C-D=b-c-4-b+a=a-c-4\)
\(A+B=C-D\)


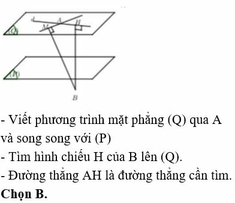

Chọn đáp án C
Lấy điểm M trên a, qua M kẻ đường thẳng b' song song với b. Khi đó mặt phẳng (a;b') song song với b.
Nếu có một mặt phẳng (P) khác (a;b') chứa a mà song song với b khi đó P ∩ a ; b ' = a phải song song với b. Mâu thuẩn a, b chéo nhau. Vậy có duy nhất một mặt phẳng chứa a và song song với b.