Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có t O m ^ = 2 t O z ^ , t O m ^ = 1 2 x O y ^
Mà góc xOy có số đo lớn nhất bằng 180° (góc bẹt) nên góc tOm có số đo lớn nhất bằng 90°. Nên m O n ^ = 150 ° - 130 ° = 20 °

Oz là phân giác \(\widehat{xOy}\)
\(\Rightarrow\)\(\widehat{xOz}=\frac{1}{2}\widehat{xOy}\)
Ot là phân giác \(\widehat{xOz}\)
\(\Rightarrow\)\(\widehat{xOt}=\frac{1}{2}\widehat{xOz}\)
\(\Leftrightarrow\)\(\widehat{xOt}=\frac{1}{4}\widehat{xOy}\)
\(\widehat{xOt}\)lớn nhất \(\Leftrightarrow\)\(\widehat{xOy}\)lớn nhất
\(\Rightarrow\)\(\widehat{xOy}=180^0\)
\(\Rightarrow\)\(\widehat{xOt}=45^0\)
Góc lớn nhất là góc 180 độ nên góc xOy =180 độ
Vì Oz là tia phan giác của góc xOy nên góc xOz = 180 độ chia 2 = 90 độ
Vì Ớt là tia phân giác của góc xOz nên góc xOt = 90 độ chia 2 = 45 độ
45 độ là giá trị lớn nhất của góc xOt

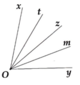
a) Theo tính chất tia phân giác của một góc, ta có:
x O z ^ = y O z ^ = 1 2 x O y ^
x O t ^ = t O z ^ = 1 2 x O z ^ (1)
z O m ^ = y O m ^ = 1 2 y O z ^
Từ đó, suy ra t O z ^ = m O z ^
Mặt khác, Ox và Ot cùng thuộc một nửa mặt phẳng bò chứa tia Oz; Oy và Om cùng thuộc nửa mặt phẳng còn lại. Do đó, tia Oz nằm giữa hai tia Ot và Om.
Vậy tia Oz là tia phân giác của góc tOm
b) Từ (1), ta suy ra t O z ^ = 1 2 x O z ^ = 1 2 . 1 2 x O y ^ = 1 4 x O y ^
Do đó, x O y ^ = 4 t O z ^
c) Từ ý a), suy ra t O m ^ = 2 t O z ^
Kết hợp với ý b), ta có t O m ^ = 1 2 x O y ^
Mà góc xOy có số đo lớn nhất bằng 180° (góc bẹt) nên góc tOm có số đo lớn nhất bằng 90°. Nên m O n ^ = 150°- 130° = 20°.

ta có góc xoz + zot = xot mà ớt là tia phân giác cua góc zoy nên ta có : (120-24):2= zot=48o góc xot = 48o+24o= 72o
chúc bạn thành công.......

Oz là phân giác góc xOy
\(\Rightarrow\)\(\widehat{xOz}=\frac{1}{2}\widehat{xOy}\) (1)
Ot là phân giác góc xOz
\(\Rightarrow\)\(\widehat{xOt}=\frac{1}{2}\widehat{xOz}\) (2)
Từ (1) và (2) suy ra: \(\widehat{xOt}=\frac{1}{4}\widehat{xOy}\)
đề góc xOt lớn nhất thì góc xOy lớn nhất
mà \(\widehat{xOy}\le180^0\)
\(\Rightarrow\)\(\widehat{xOy}=180^0\)
Vậy \(\widehat{xOt}=45^0\)