Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tham khảo ở đây nhé
Cho góc nhọn xOy. Điểm H nằm trên đường phân giác góc xOy. Từ H dựng các đường vuông góc với 2 cạnh Ox, Oy. Chứng minh tam giác HAB cân - Toán học Lớp 7 - Bài tập Toán học Lớp 7 - Giải bài tập Toán học Lớp 7 | Lazi.vn - Cộng đồng Tri thức & Giáo dục

a: Xét ΔOKB vuông tại K và ΔOHA vuông tại H có
OB=OA
\(\widehat{O}\) chung
Do đó: ΔOKB=ΔOHA
Suy ra: OK=OH
hay ΔOHK cân tại O

a: Xét ΔOKB vuông tại K và ΔOHA vuông tại H có
OB=OA
\(\widehat{O}\) chung
Do đó: ΔOKB=ΔOHA
Suy ra: OK=OH
hay ΔOHK cân tại O

a: Xét ΔOHA vuông tại H và ΔOKB vuông tại K có
OA=OB
\(\widehat{O}\) chung
Do đó: ΔOHA=ΔOKB
Suy ra: OH=OK

O x y z C E B A H
Xét tam giác AHO và tam giac BHO
có góc AOH = góc BOH (GT)
OH chung
góc OHA=góc OHB = 90 độ
suy ra tam giác AHO = tam giac BHO (G.C.G)
suy ra OA=OB(hai cạnh tương ứng) , HA=HB (hai cạnh tương ứng)
b) Vì góc AOB = 1000
mầ tia OH là phân giác của góc AOB
suy ra góc AOH = góc BOH =góc AOB:2=500
LẠi có OA=OB suy ra tam giác AOB cân tại O
suy ra góc ABO=góc BAO
Trong tam giác AOB có góc ABO+góc BAO +1000= 1800
suy ra góc ABO=góc BAO=400
c) Xét tam giác HBC và tam giác HAC
có BH=HA (CMT)
góc AHC=góc BHC=900
HC chung
suy ra tam giác HBC = tam giác HAC (c.g.c)
suy ra BC=CA suy ra tam giác ABC cân tại C
mà góc HBC = 600
suy ra tam giác ABC đều.
d) Xét tam giác AOB và tam giác EBO
có BE=OA=BO
góc EBO=góc AOB=1000
OB chung
suy ra tam giác AOB =tam giác EBO
suy ra AB=OE (hai cạnh tương ứng)
a)Xét hai t/g vuông OHA và OHB có:
OH(chung)
góc HOA=góc HOB(gt)
=>T/g OHA = t/g OHB(cạnh góc vuông-góc nhọn kề)
=>HA=HB;OA=OB
b)Vì OB=OA(câu a) nên t/g OAB cân tại O
=>Góc A=góc B
Do đó:
A=B=(180-O):2
=(180-100):2=40

a) xet tam giac OAH va tam giac OBH : OH=OH ( canh chung ), OA=OB (gt), goc HOA= goc HOB( Ot la tia p/g goc xOy)-> tam giac = nhau (c-g-c)
b) cm tam giac OHB= tam giac AHC (c=g=c) ; OH=HC , BH=AH (tam giac OAH=tam giac OBH), goc OHB= goc CHA( 2 goc doi dinh)
c) C1 : cm tam giac OAB can tai O co OH la phan giac -> OH la duong cao -> OH vuong goc AB hay OC vuong goc AB
C2 : ta co : goc OHB+ goc OHA=180 ( 2 goc ke bu)
goc OHB= goc OHA( tam giac OHA= tam giac OHB )
--> goc OHB+goc OHB=180
-> 2 gpc OHB=180
->goc OHB=180:2=90
-> OH vuong goc AH tai H hay OC vuong goc AB

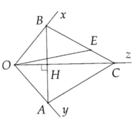
O A B H x y z
Ta có: ^HBx là góc ngoài của tam giác OBH => ^HBx=^BOH+^OHB=^BOH+900 (1)
^ABx là góc ngoài tam giác OBA => ^ABx=^AOB+^OAB=1/2^BOH+450 (2)
Từ (1) và (2) => ^ABx=1/2^HBX (Vì 1/2^BOH+450=(^BOH+900)/2)
=> BA là tia phân giác ^HBx.
Xét tam giác BOH: OA là phân giác trong, BA là phân giác ngoài.
2 tia trên cắt nhau tại A => HA là phân giác ngoài của tam giác BOH.
Hay HA là phân giác ^BHy (đpcm)