Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải :
a, Ox là đường trung trực của AB nên OA=OB
Oy là đường trung trực của AC nên OA=OC
=> OB=OC
b, Xét tg AOB cân tại O ( do OA=OB )
=> góc O1= góc O2 = 1/2 góc AOB
Xét tg AOC cân tại o ( vì OA=OC )
=> góc O3 = góc O4 = 1/2 góc AOC
nên góc AOB+ góc AOC= 2 (góc O1+góc O3)
= 2.góc xOy
= 2.60 độ
= 120 độ
Vậy góc BOC = 120 độ
( Hình thì dễ nên bạn tự vẽ nhé )

a/ Xét tam giác OAC và tam giác OBD có
O : góc chung
OA = OB (GT)
OC = OD (GT)
=> tam giác OAC = tam giác OBD ( cạnh góc cạnh )
=>AC = BD (2 cạnh tương ứng)
b/ Xét tam giác IAD và IBC có
-góc C = góc D (vì tam giác OAC=tam giác OBD)
-A = B = 900
-AI = BI (vì AC = BD)
=> tam giác IAD = tam giác IBC (góc cạnh góc)
=>AD=BC (2 cạnh tương ứng)
c/ Xét tam giác OAI và tam giác OBI có
-OA = OB (GT)
-góc AIO = góc OIB
-A = B = 900
=> tam giác OAI = tam giác OBI (cạnh góc cạnh)
=> góc AOI = góc IOB (2 góc tương ứng)
Vậy OI là phân giác của góc O
d/ Gọi OI và AB cắt nhau tại M
Xét tam giác OAM và tam giác OBM có
-AOM = BOM
-OA = OB
-OM: cạnh chung
=> tam giác OAM = tam giác OBM (cạnh góc cạnh)
=> AMO = BMO
Ta có: AMO + BMO = 1800 (kề bù)
Mà AMO = BMO
=> AMO = BMO = 1/2 1800 = 900
Vậy OI là đường trung trực của đoạn AB
e/ Gọi phân giác của góc O cắt CD tại N
Xét tam giác INC = tam giác IND có
IN: cạnh chung
DIN = CIN
ID = IC
=> tam giác INC = tam giác IND (cạnh góc cạnh)
=> INC = IND
Ta có; IND + INC =1800 (kề bù)
Mà INC = IND
=> INC =IND = 1/2 1800 = 900
=> IN là trung trực của CD
Ta có: IN là trung trực của CD
OI là trung trực của AB
=> AB//CD

. . A B // // C _ _ O x y H K
a) Gọi giao điểm của Oy và AC là H, giao điểm của Ox và AB là K
Nối O với A
Xét \(\Delta OHC\)và\(\Delta OHA\)có:
\(\widehat{OHC}=\widehat{OHA}\)\(\left(=90^o\right)\)
\(OH\)là cạnh chung
\(HC=HA\)(H là trung điểm của AC)
\(\Rightarrow\Delta OHC=\Delta OHA\left(c.g.c\right)\)
\(\Rightarrow OC=OA\)(2 cạnh tương ứng) (1)
Xét \(\Delta OKA\)và \(\Delta OKB\)có:
\(\widehat{OKA}=\widehat{OKB}\left(90^o\right)\)
\(OK\)là cạnh chung
\(KA=KB\)(K là trung điểm của AB)
\(\Rightarrow\Delta OKA=\Delta OKB\left(c.g.c\right)\)
\(\Rightarrow OA=OB\)(2 cạnh tương ứng) (2)
Từ (1) và (2) \(\Rightarrow OC=OB\)
b) Vì \(\Delta OHC=\Delta OHA\)(Chứng minh trên)
\(\Rightarrow\widehat{COH}=\widehat{AOH}\)
\(\Rightarrow\)\(OH\)là tia phân giác \(\widehat{COA}\)
\(\Rightarrow\widehat{COA}=2\widehat{AOH}\)
Vì\(\Delta OKA=\Delta OKB\)(Chứng minh trên)
\(\Rightarrow\widehat{AOK}=\widehat{BOK}\)
\(\Rightarrow OH\)là tia phân giác \(\widehat{AOB}\)
\(\Rightarrow\widehat{AOB}=2\widehat{AOK}\)
Ta có:\(\widehat{COA}+\widehat{AOB}=\widehat{BOC}\)
\(\Rightarrow2\widehat{AOH}+2\widehat{AOK}=\widehat{BOC}\)
\(\Rightarrow2\left(\widehat{AOH}+\widehat{AOK}\right)=\widehat{BOC}\)
\(\Rightarrow2.\widehat{HOK}=\widehat{BOC}\)
\(\Rightarrow2.60^o=\widehat{BOC}\)\(\left(\widehat{xOy}=\widehat{HOK}=60^o\right)\)
\(\Rightarrow\widehat{BOC}=120^o\)
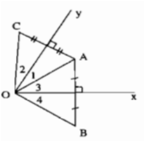
Vì ΔOAB cân tại O và Ox là đường trung trực của AB nên Ox là đường phân giác của ∠(AOB) (tính chất tam giác cân)
Suy ra: ∠O3 = ∠O4 (3)
Vì tam giác OAC cân tại O và Oy là đường trung trực của AC nên Oy là đường phân giác của ∠(AOC) (tính chất tam giác cân)
Suy ra: ∠O1 = ∠O2 (4)
Từ (3) và (4) suy ra: ∠O1 + ∠O3 = ∠O2 + ∠O4
Ta có: ∠(BOC) = ∠O1 + ∠O3 + ∠O2 + ∠O4
= 2(∠O1 + ∠O3 ) = 2.∠(xOy) = 2.60o = 120o.