Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha!
a) Vì tia OH là tia phân giác của \(\widehat{xOy}\)
\(\Rightarrow\) \(\widehat{xOH}\)=\(\widehat{yOH}\)hay \(\widehat{AOH}\)=\(\widehat{BOH}\)\((\)vì A\(\in\)Ox,B\(\in\)Oy\()\)
Xét tam giác AOH và tam giác BOH, có:
\(\widehat{AOH}\)=\(\widehat{BOH}\)
OH chung
\(\widehat{OHA}\)=\(\widehat{OHB}\)(=\(^{90^0}\))
\(\Rightarrow\)Tam giác AOH= Tam giác BOH (g-c-g)
\(\Rightarrow\)\(\hept{\begin{cases}HA=HB\\OA=OB\end{cases}}\)
Vậy....

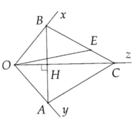
O x y z C E B A H
Xét tam giác AHO và tam giac BHO
có góc AOH = góc BOH (GT)
OH chung
góc OHA=góc OHB = 90 độ
suy ra tam giác AHO = tam giac BHO (G.C.G)
suy ra OA=OB(hai cạnh tương ứng) , HA=HB (hai cạnh tương ứng)
b) Vì góc AOB = 1000
mầ tia OH là phân giác của góc AOB
suy ra góc AOH = góc BOH =góc AOB:2=500
LẠi có OA=OB suy ra tam giác AOB cân tại O
suy ra góc ABO=góc BAO
Trong tam giác AOB có góc ABO+góc BAO +1000= 1800
suy ra góc ABO=góc BAO=400
c) Xét tam giác HBC và tam giác HAC
có BH=HA (CMT)
góc AHC=góc BHC=900
HC chung
suy ra tam giác HBC = tam giác HAC (c.g.c)
suy ra BC=CA suy ra tam giác ABC cân tại C
mà góc HBC = 600
suy ra tam giác ABC đều.
d) Xét tam giác AOB và tam giác EBO
có BE=OA=BO
góc EBO=góc AOB=1000
OB chung
suy ra tam giác AOB =tam giác EBO
suy ra AB=OE (hai cạnh tương ứng)
a)Xét hai t/g vuông OHA và OHB có:
OH(chung)
góc HOA=góc HOB(gt)
=>T/g OHA = t/g OHB(cạnh góc vuông-góc nhọn kề)
=>HA=HB;OA=OB
b)Vì OB=OA(câu a) nên t/g OAB cân tại O
=>Góc A=góc B
Do đó:
A=B=(180-O):2
=(180-100):2=40

1.Tự vẽ hình ha!
Cm:
a) Xét \(\Delta OAD\)và \(\Delta OCB\)có:
OA=OC (gt)
OD=OB (gt)
\(\widehat{O}\)chung
=>\(\Delta OAD\)=\(\Delta OCB\)(c.g.c)
=>AD=BC (2 cạnh tương ứng) (Đpcm)
b) Vì\(\Delta OAD\)=\(\Delta OCB\)(cmt) => \(\widehat{ODA}=\widehat{OBC};\widehat{OAD}=\widehat{OCB}\)(2 góc t/ứ)
Ta có: \(\widehat{OAD}+\widehat{DAB}=180^0\)(2 góc kề bù)
\(\Rightarrow\widehat{DAB}=180^0-\widehat{OAD}\)
Lại có: \(\widehat{OCB}+\widehat{BCD}=180^0\)(2 góc kề bù)
\(\Rightarrow\widehat{BCD}=180^0-\widehat{OCB}\)
Mà \(\widehat{OAD}=\widehat{OCB}\)(cmt)
\(\Rightarrow\widehat{DAB}=\widehat{BCD}\)hay \(\widehat{IAB}=\widehat{ICD}\)
Ta có: OA=OC;OB=OD (GT)
=> OB-OA=OD-OC
=>AB=CD
Xét\(\Delta AIB\) và\(\Delta CID\)có:
AB=CD (cmt)
\(\widehat{IAB}=\widehat{ICD}\)(cmt)
\(\widehat{ODA}=\widehat{OBC}\)(cmt)
=>\(\Delta AIB\)=\(\Delta CID\)(g.c.g)
=>AI=IC; IB=ID (đpcm)
c) Xét \(\Delta OID\)và\(\Delta OIB\)có:
OD=OB (gt)
ID=IB (cmt)
\(\widehat{ODA}=\widehat{OBC}\)(cmt)
=>\(\Delta OID\)=\(\Delta OIB\)(c.g.c)
=>\(\widehat{DOI}=\widehat{BOI}\)
=> OI là tia pg của góc xOy (đpcm)