Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

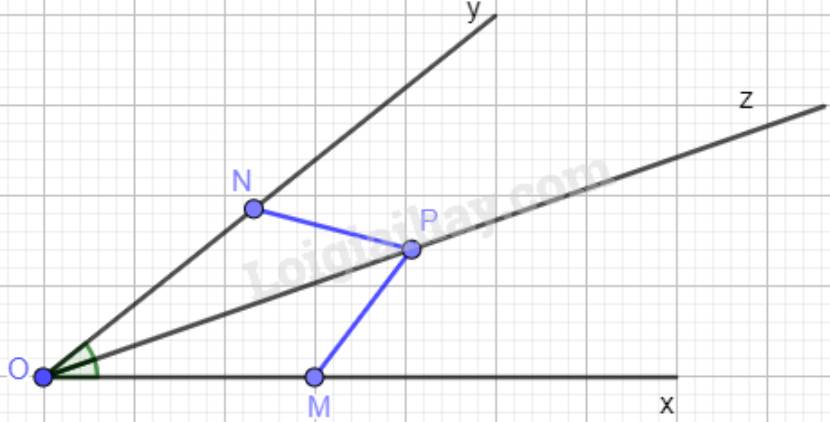
Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).
Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)
\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)

a) ta có \(OP+PQ=OQ\)
\(OM+MN=ON\)
mà \(OP=OM;PQ=MN\)
\(\Rightarrow OQ=ON\)
Xét \(\Delta NOPvà\Delta QOMcó\)
\(OP=OM\) ( giả thiết )
\(\widehat{QON}\) là góc chung
\(OQ=ON\) (chứng minh trên)
\(\Rightarrow\Delta NOP=\Delta QOM\left(c-g-c\right)\)
vậy \(\Delta NOP=\Delta QOM\)
b) tự làm nhé

Xét ΔOQM và ΔOPN có
OQ=OP
góc O chung
OM=ON
=>ΔOQM=ΔOPN
=>góc OQM=góc OPN

a: Trên tia Ox, ta có: OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN+4=8
=>MN=4(cm)
b: Ta có: M nằm giữa O và N
MN=MO(=4cm)
Do đó: M là trung điểm của ON
c: Trên tia Ox, ta có: OP<OM
nên P nằm giữa O và M
=>OP+PM=OM
=>PM+2=4
=>PM=2(cm)
Ta có: P nằm giữa O và M
mà OP=PM(=2cm)
nên P là trung điểm của OM
Trên tia Ox, ta có: OM<OQ
nên M nằm giữa O và Q
=>OM+MQ=OQ
=>MQ+4=6
=>MQ=2(cm)
Vì MP=MQ(=2cm)
nên M là trung điểm của PQ
Trên tia Ox, ta có: OQ<ON
nên Q nằm giữa O và N
=>OQ+QN=ON
=>QN+6=8
=>QN=2(cm)
Vì MQ=QN(=2cm)
nên Q là trung điểm của MN

a. Xét tam giác MOA và tam giác MOB có :
OM là cạnh chung
MOA = MOB ( vì ox là tia phân giác góc xOy )
OMA = OMB ( = 90 độ )
Nên tam giác MOA = tam giác MOB ( c - c - c )
b. Ta có tam giác MOA = tam giác MOB ( cmt )
Nên MA = MB
Do đó M là trung điểm của AB
Vì vậy OM là đường trung trực của AB
Nhớ tk mk nha !!!
Xét tam giác AMO vuông tại A và tam giác BMO vuông tại B có:
AOM = BOM (OM là tia phân giác của AOB)
OM chung
=> Tam giác AMO = Tam giác BMO (cạnh huyền - góc nhọn)
=> AMO = BMO (2 góc tương ứng) => MO là tia phân giác của AMB
AM = BM (2 cạnh tương ứng) => tam giác MAB cân tại A
có MO là tia phân giác của AMB (chứng minh trên)
=> MO là đường trung trực của AB

Ta có hình vẽ:
x O y t Q M H G
Cho Ot là tia phân giác \(\widehat{xOy}\)
a/ Xét tam giác OQM và tam giác OHM có:
\(\widehat{QOM}\)=\(\widehat{HOM}\) (GT)
OM: cạnh chung
\(\widehat{Q}\)=\(\widehat{H}\) =900 (GT)
Vậy tam giác OQM = tam giác OHM
(theo trường hợp cạnh huyền góc nhọn)
=> MQ = MH (2 cạnh tương ứng)
b/ Xét tam giác OQG và tam giác OHG có:
OG: cạnh chung
\(\widehat{QOM}\)=\(\widehat{HOM}\) (GT)
MQ = MH (câu a)
Vậy tam giác OQG = tam giác OHG (c.g.c)
=> GQ = GH (2 cạnh tương ứng)
c/ Ta có: tam giác OQG = tam giác OHG (đã chứng minh trên)
=> \(\widehat{OGQ}\)=\(\widehat{OGH}\) (2 góc tương ứng)
Mà \(\widehat{OGQ}\)+\(\widehat{OGH}\)=1800 (kề bù)
=> \(\widehat{OGQ}\)=\(\widehat{OGH}\)=900 (1)
Ta lại có: GQ = GH (đã chứng minh ở câu b) (2)
Từ (1),(2) => OG là đường trung trực của QH
hay OM là đường trung trực của QH
(vì G,M đều nằm trên tia phân giác Ot)

a) vì C thuộc đường phân giác góc xOy =) CM =CN (theo tính chất tia phân giác của 1 góc )
b)Xét tam giác CME và tam giác CNF có CM =CN ;góc M =góc N 90 độ ;goc ECM =góc FCN =) 2 tam giác bằng nhau
=)CF=CE (cạnh tương ứng )
c) có tam giác MCO vuông =) MO2+MC2=OC 2=) MC2=MO2_ CO2 = 132- 122=252=) MC =\(\sqrt{25}\) =5 ; -5
VÌ MC >0 =) MC =5
O C M N E F Y X
Xét tam giác OMQ và tam giác OPN có: OM = OP (= 2 cm); OQ = ON (= 3 cm); góc O chung.
Vậy \(\Delta OMQ = \Delta OPN\) (c.g.c)
\(\Rightarrow MQ = NP\) ( 2 cạnh tương ứng)