Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/Xét tam giác OCA và tam giác OCB:
OC chung
OAC=OBC(90 độ)
Góc AOC=BOC(Phân giác Oz)
=> Tam giác OCA=OCB(ch-gn)
=> CA=CB(cạnh tương ứng)
b/ Xét tam giác CAF và tam giác CBE:
Góc ACF=BCE(đối đỉnh)
Góc CBE=CAF(90 độ)
AC=CB(câu a)
=> Tma giác CAF=tam giác CBE(ch-gn)
=> CF=CE(cạnh tương ứng)
=> Tam giác CEF cân tại C
c/Xét tam giác vuông CBE có:
CE là cạnh huyền.
=> CE>CB Mà CB=CA
=> CE>CA(đpcm)
Bạn tự vẽ hình nha![]()
b.
Xét tam giác AFC và tam giác BEC có:
FAC = EBC ( = 90 )
AC = BC (theo câu a)
ACF = BCE (2 góc đối đỉnh)
=> Tam giác AFC = Tam giác BEC (g.c.g)
=> CF = CE (2 cạnh tương ứng)
=> Tam giác CEF cân tại C
c.
Tam giác BCE vuông tại B có:
BC < CE (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà BC = AC (theo câu a)
=> AC < CE
Chúc bạn học tốt![]()

câu a/ bạn biết rồi thì tui giải câu b và c
b/ Ta có tam giác CAE=tam giác CBF(cgv-gnk)
suy ra CE=CF
Vậy tam giác CEF cân tại C.
c/ Trong tam giác vuông cạnh huyền là cạnh lớn nhất nên AC<CE(cgv<ch).
Câu b mình gợi ý cậu xét hai tam giác BC và tam giác CAF
Rồi từ đó => CE = CF ( vì hai cạnh tương ứng )
Vậy tam giác CEF cân ( vì CE = CF )
Còn câu c mình không biết nữa

a: Xét ΔOAC vuông tại A và ΔOBC vuông tại B có
OC chung
góc AOC=góc BOC
=>ΔOAC=ΔOBC
b: Xét ΔCAD vuông tại A và ΔCBE vuông tại B có
CA=CB
góc ACD=góc BCE
=>ΔCAD=ΔCBE
=>CE=CD và AD=BE
c: Xét ΔOED có OA/AD=OB/BE
nên AB//ED

Xét \(\Delta OAB\)và \(\Delta OAC\)có :
\(\widehat{OBA}=\widehat{OCA\left(=90^o\right)}\)
OA là cạnh chung
\(\widehat{O_1}=\widehat{O_2}\left(gt\right)\)
\(\Rightarrow\Delta OAB=\Delta OAC\left(ch-gn\right)\)
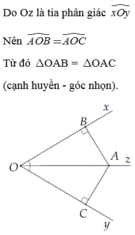
xét tam giác AOB và tam giác AOC có:
AO chung
\(\widehat{AOB}\)=\(\widehat{AOC}\)(gt)
\(\Rightarrow\)tam giác AOB=tam giác AOC(CH-GN)
\(\Rightarrow\)AB=AC đpcm