Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét △OAC vuông tại A và △OBD vuông tại B
Có: OA = OB (gt)
COA = DOB (2 góc đối đỉnh)
=> △OAC = △OBD (cgv-gnk)
b, Xét △OCE và △ODE cùng vuông tại O
Có: OE là cạnh chung
OC = OD (△OAC = △OBD)
=> △OCE = △ODE (2cgv)
c, Ta có: DE = BE + BD mà BD = AC (△OBD = △OAC) ; CE = DE (△OCE = △ODE)
=> CE = BE + AC (đpcm)
ý AC = 1/2 BC còn có điều kiện gì nữa ko??

30 o O x y z m n
Bài làm
Vì Om là tia phân giác của \(\widehat{xOy}\)
=> \(\widehat{xOm}=\widehat{mOy}=\frac{\widehat{xOy}}{2}=\frac{30^0}{2}=15^0\)
Vì On là tia phân giác của \(\widehat{xOz}\)
=> \(\widehat{xOn}=\widehat{nOz}=\frac{\widehat{xOz}}{2}=\frac{120^0}{2}=60^0\)
Ta có: \(\widehat{xOm}+\widehat{mOn}+\widehat{nOz}=\widehat{xOz}\)
hay \(15^0+\widehat{mOn}+60^0=120^0\)
=> \(\widehat{mOn}=120^0-15^0-60^0\)
=> \(\widehat{mOn}=45^0\)
Vậy \(\widehat{mOn}=45^0\)
# Học tốt #
Bài giải
O x y 30 o z 120 o m n
a) Vì \(\widehat{xOy}\) < \(\widehat{xOz}\) ( 30 độ < 120 độ ) => Tia Oy nằm giữa hai tia còn lại.
Vì tia Oy nằm giữa hai tia Ox và Oz nên
\(\widehat{\text{yOz}}\) + \(\widehat{\text{xOy}}\) = \(\widehat{\text{xOz}}\)
=> \(\widehat{\text{yOz}}\) = \(\widehat{\text{xOz}}\) − \(\widehat{\text{xOy}}\) = 120 độ - 30 độ = 90 độ
Vậy \(\widehat{\text{yOz}}\)= 90 độ
b) Vì Om là tia phân giác của góc \(\widehat{\text{xOy}}\) nên
\(\widehat{xOm}\) = \(\widehat{\text{xOy}}\) : 2 = 30 độ : 2 =15 độ
Vì On là tia phân giác của góc \(\widehat{\text{yOz }}\) nên
\(\widehat{\text{xOn}}\) = \(\widehat{\text{xOz}}\): 2 = 120 độ : 2 = 60 độ
Vì \(\widehat{\text{xOm}}\) và \(\widehat{\text{xOn}}\) cùng nằm trên một nửa mặt phẳng chứa tia Ox và \(\widehat{\text{xOm}}\) < \(\widehat{\text{xOn}}\) => Tia Om nằm giữa hai tia On và Ox- Ta có : \(\widehat{\text{xOm}}\) + \(\widehat{\text{mOn}}\) = \(\widehat{\text{xOn}}\)=> ^mOn = ^xOn − ^xOm = 60 độ - 15 độ = 45 độ
Vậy \(\widehat{mon}\) = 45 độ

a) ta có: góc xOy + góc OAt = 120 độ + 60 độ = 180 độ
mà góc xOy ; góc OAt nằm ở vị trí trong cùng phía
=> tt' // Oy ( định lí //)
b) ta có: tt' // Oy ( phần a)
=> góc xOy = góc xAt ( so le trong)
mà góc AOm = góc xOy/2 ( định lí tia phân giác)
góc xAn = góc xAt/2 ( định lí tia phân giác)
=> góc AOm = góc xAn ( = góc xOy/2 = góc xAt/2)
mà góc AOm ; góc xAn nằm ở vị trí đồng vị
=> Om // An ( định lí //)
bn tự kẻ hình nha

Bài giải
x y O 140 0 z m n
a, Hai góc \(xOz\) và \(yOz\) kề bù nên :
\(\widehat{xOz}+\widehat{yOz}=180^o\)
\(\widehat{xOz}+140^o=180^o\)
\(\widehat{xOz}=180^0-140^0\)
\(\widehat{xOz}=40^o\)
b, Om là tia phân giác của góc \(xOz\) \(\Rightarrow\text{ }\widehat{xOm}=\widehat{mOz}=\frac{1}{2}\cdot\widehat{xOz}=\frac{1}{2}\cdot40=20^0\)
On là tia phân giác của góc \(yOz\text{ }\Rightarrow\text{ }\widehat{yOn}=\widehat{nOz}=\frac{1}{2}\cdot\widehat{yOz}=\frac{1}{2}\cdot140^0=70^0\)
\(\Rightarrow\text{ }\widehat{xOm}+\widehat{mOz}+\widehat{yOn}+\widehat{nOz}=180^0\)
\(\widehat{mOz}+\widehat{nOz}=180^0-\widehat{xOm}-\widehat{yOn}\)
\(\widehat{mOz}+\widehat{nOz}=180^0-20^0-70\)
\(\widehat{mOz}+\widehat{nOz}=90^0\)
Vì hai góc \(mOz\) và \(nOz\) kề nhau , cùng nằm trên một nửa mặt phẳng và \(\widehat{mOz}+\widehat{nOz}=90^0\)
\(\Rightarrow\text{ }\text{OM vuông góc với ON}\)
a) Vì đ 0 nằm trên đgt xy => xOz kề bù với yOz => xOz + yOz = 180
Thay số : xOz + 140 = 180
xOz = 180 - 140 = 40
b) Vì Om là tia p giác của xOz => xOm = mOz = xOz / 2
Vì On là tia p giác của zOy => zOn = nOy = zOy / 2
Có: xOz và yOz là 2 góc kề bù => xOz + yOz = 180
\(\Rightarrow\) mOn = mOz + nOy
= xOz/2 + zOy/2
= (xOz + zOy) /2
= 180 /2
= 90
Suy ra mOn là góc vuông \(\Rightarrow\) Om vuông góc với On (Điều Phải Chứng Minh)
chọn (k) đúng cho mình nha
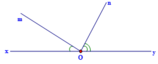
+) Ta có: x O m ^ = 30 0 , y O n ^ = 2 x O m ^ = 2.30 0 = 60 0
Vì x O m ^ + m O y ^ = x O y ^ = 180 0 (hai góc kề bù)
=> m O y ^ = 180 0 − x O m ^ = 180 0 − 30 0 = 150 0
+) Xét trên nửa mặt phẳng có bờ chứa tia Oy, có : y O n ^ < y O m ^ (vì 0 ° < 60 ° < 150 ° )
=> Tia On nằm giữa hai tia Oy và Om
⇒ m O n ^ + n O y ^ = m O y ^ = 150 0 ⇒ m O n ^ + 60 0 = 150 0 ⇒ m O n ^ = 150 0 − 60 0 ⇒ m O n ^ = 90 0 ⇒ O m ⊥ O n .