Question

[Trần Thị Tuý Nga]

Cho G là trọng tâm của Tam giác đều ABC. Trên tia AG lấy K sao cho G là trung điểm của AK. Chứng minh rằng BGK là tam giác đều.

Vẽ hình giùm mik đi ạ 

Answer 1

[Nguyễn Việt Lâm]

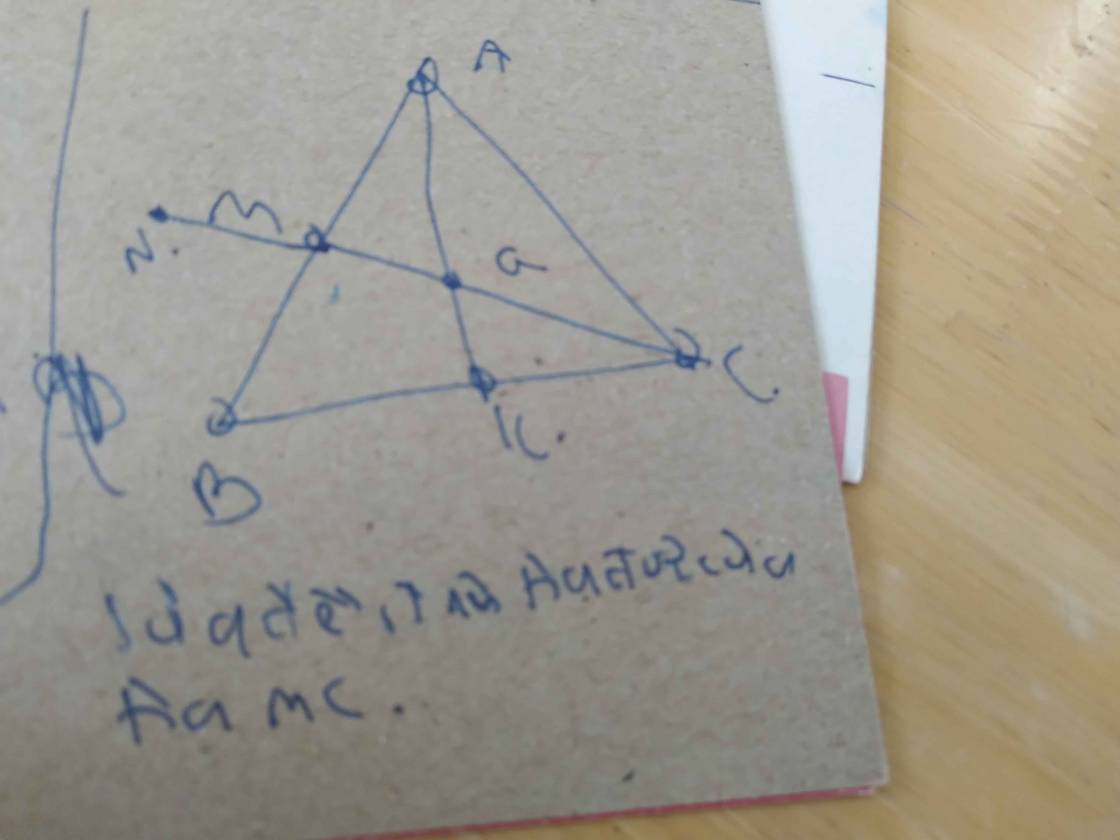
Đặt \(AB=BC=CA=a\)

Gọi D là trung điểm BC \(\Rightarrow AG=BG=\dfrac{2}{3}AD\) và \(DG=\dfrac{1}{3}AD\)

G là trung điểm AK \(\Rightarrow GK=AG=\dfrac{2}{3}AD\Rightarrow GK=BG\) (1)

\(DG+DK=GK\Rightarrow DK=GK-DG=\dfrac{1}{3}AD\Rightarrow DK=DG\) \(\Rightarrow\) BD là trung tuyến của tam giác BGK

Mặt khác tam giác ABC đều \(\Rightarrow AD\perp BC\) \(\Rightarrow\) BD là đường cao của tam giác BGK

Xét tam giác BGK có BD đồng thời là trung tuyến và đường cao

\(\Rightarrow\Delta BGK\) cân tại B \(\Rightarrow BG=BK\) (2)

Từ (1), (2) \(\Rightarrow BG=BK=GK\Rightarrow\Delta BGK\) là tam giác đều